Двокаскадна декомпозиція простору

Підхід з декомпозицією всього простору n -вимірних даних полягає в поділі всіх координат на частини і побудови гіперкубів. Фактично рознесення значень точок n -вимірного простору у відповідний гіперкуб вимагає попереднього опрацювання даних, а саме сортування значень вибірки за всіма координатами.

Для декомпозиції простору використовуємо двокаскадну кластеризацію. Розбиваємо вхідну множину ключів Q (Q ₁, Q ₂, Q ₃, … Q_N)на p підмножин O ₁(Q ₁, Q ₂, Q ₃, … Q_z), O ₂(Q_{z+ 1}, Q _{z +2}, Q _{z +3}, … Q_t), …, O_p (Q_{t +1}, Q _{t +2}, Q_{t+ 3}, … Q_N). До кожної з підмножин, застосуємо алгоритм кластеризації, утворивши множини відповідних кластерів K ₁(k ₁, k ₂, k ₃, …), K ₂(k_s, k_{s +1}, k_{s +2}, …), …, K_p (k_r, k_{r +1}, k_{r +2}, …), де k ₁, k ₂, …, k_i,... – кластери, ключі в яких відносяться до відповідних підмножин O ₁, O ₂, …, O_p. Утворимо множину кластерів 1-го каскаду кластеризації K об’єднанням (2.20). Застосуємо до цієї множини алгоритм кластеризації, розглядаючи кожен з кластерів k ₁, k ₂, …, k_i,... як базовий, тобто листок деревазгортання. В результаті сформується множина кластерів 1-го каскаду. Таким чином отримуємо двокаскадну декомпозицію простору. Схема поділу та згортання зображена на рис. 2.10.

Рис. 2.10. Двокаскадне дерево формування кластерів

Нехай простір складаєтсься із s n -вимірних даних: C = C (a, b, …, z). Вимірність а поділимо на n частин, b – на m частин,..., вимірність z – на k частин. Поділ простору за вимірностями на частини за параметрами n, m, …, k позначимо вектором розбиття l = (n, m, …, k). Схематично поділ тривимірного простору зображено на рис. 2.11.

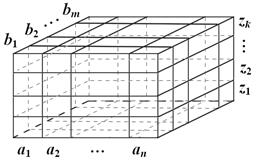
Рис. 2.11. Схема поділу тривимірного простору на куби

Використаємо два способи поділу простору: гіперкуби різних розмірів, але з однаковою кількістю значень даних; другий ­­– на гіперкуби з неконтрольованими кількостями значеннями даних, але контрольованими розмірами сторін, що задаються користувачем.

На рис. 2.12 схематично зображено поділ двовимірного простору: а – вхідна множина, б – гіперкуби із однаковою кількістю точок, в – поділ за значеннями по кожній координаті.

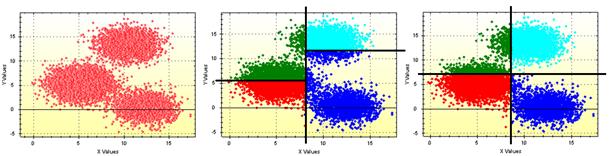
а б в

Рис. 2.12. Схема поділу двовимірного простору

На рис. 2.12, а зображено простір що складається із 20000 2-вимірних точок, згенерованих за нормальним законом розподілу. На рис. 2.12, б вектор розбиття l = (2, 2) дає гіперкуби (прямокутники у 2-вимірному просторі) із однаковою кількістю точок, але різних за розмірами. На рис. 2.12, в цей же вектор розбиття та поділ координатних проміжків на рівні частини дає однакові гіперкуби. На рис. 2.12, б – кожна підмножина (кожен квадрант) містить по 5000 точок. На рис. 2.12, в червоним кольором позначено 4540 точок, зеленим – 2030, синім – 11350, темносинім – 2080.

Складність алгоритму збільшується на сортування вибірки за всіма координатами, тобто стає рівною: O (p ∙ n_i ³) + p ∙ O (N ²).

Приведемо алгоритм поділу гіперкуба на куби із однаковою кількістю точок:

Крок 0. Отримати вектор l = (n, m, …, k) розбиття гіперкуба за його вимірностями a, b, …, z; i = 0; множина C – вхідна множина.

Крок 1. Обчислити count = [ s / l ₀].

Крок 2. Якщо l ₀ = 1 то перейти на крок 7, інакше на крок 3.

Крок 3. Посортувати множину С за i -вимірністю.

Крок 4. j = 0. Поки j < l ₀:

Крок 5. Поки кількість точок у C_tj не рівна count, перенести точку із множини С у C_tj, якщо С = 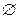перейти на крок 6, інакше j = j +1.

Крок 6. Перенести всі точки із множини С у C_tj.

Крок 7. Додати до множини С_t множину С.

Крок 8. Видалити зі списку l перший елемент l ₀.

Крок 9. Якщо l = 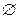, то кожну підмножину з С_t додати до множини результату С_res. Інакше i = i +1, для кожної підмножини С_t виконати алгоритм, починаючи з 1 кроку.

Множина С_t містить підмножини проміжних результатів поділу гіперкуба. Множина С_res містить шукані підмножини розбиття гіперкуба. Крок 6 додає { s / l ₀} точок до останньої підмножини у С_t.

У випадку коли необхідно поділити гіперкуб на куби за значеннями точок по кожній вимірності, поданий вище алгоритм зміниться в наступному кроці:

Крок 5. minMaxValue = C _{0, i} + C_{s -1, i}. Поки координата точки С_і ≤ [(i + 1) ∙ minMaxValue / l ₀], перенести точку із множини С у C_tj, якщо С = перейти на крок 6, інакше j = j +1.