Families of circles

A great deal can be done toward the visualization of linear transformation by the introduction of certain families of circles which may be thought of as coordinate lines in a circular coordinate system.

Consider a linear transformation of the form

w=k .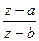

Here z=a corresponds to w=0 and z=b to w=∞. It follows that the straight lines through the origin of the w-plane are images of the circles through a and b. On the other hand, the concentric circles about the origin |w|=ρ correspond to circles with the equation | 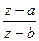|= ρ.

These are the circles of Apollonius with limit points a and b. By their equation they are the loci of points whose distances from a and b have a constant ratio.

Denote by C₁ the circles through a, b and by C₂ the circles of Apollonius with these limit points. The configuration formed by all the circles C₁ and C₂ will be referred to as the circular net or the Steiner circles determined by a and b. It has many interesting properties of which we shall list a few:

1. There is exactly one C₁ and one C₂ through each point in this plane with the exception of the limit points.

2. Every C₁ meets every C₂ under right angles.

3. Reflection in a C₁ transforms every C₂ into itself and every C₁ into another C₁. Reflection in a C₂ transforms every C₁ into itself and every C₂ into another C₂.

4. The limit points are symmetric with respect to each C₂ but not with respect to any other circle.

These properties are all trivial when the limit points are 0 and ∞, i.e. when the C₁ are lines through the origin and the C₂ concentric circles. Since the properties are invariant under linear transformation, they must continue to hold in the general case.

If a transformation w=T₂ carries a, b into a’, b’, it can be written in the form

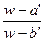=k .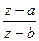

It is clear that T transforms the circles C₁ and C₂ into circles C and C₂ with the limit points a’, b’.

The situation is particularly simple is a’=a, b’=b. Then a, b are said to be fixed points of T and it is convenient to represent z and Tz in the same plane. Under these circumstances, the whole circular net will be mapped upon itself. The value of k serves to identify the image circles C and C . Indeed, with appropriate orientations C₁ forms the angle arg k with its image C , and the quotient of the constant ratios |z-a|/|z-b| on C and C₂ is |k|.

The special cases in which all C₁ or all C₂ are mapped upon themselves are particularly important. We have C =C₁ for all C₁ if k > 0 (if k > 0, the circles are still the same, but the orientation is reversed). The transformation is then said to be hyperbolic. When k increases, the points Tz, z≠ a, b will flow along the circles C₁ toward b. The consideration of this flow provides a very clear picture of a hyperbolic transformation.

The case C =C₂ occurs when |k|=1. Transformations with this property are called elliptic. When arg k varies, the points Tz move along the circles C₂. The corresponding flow circulates about a and b in different directions.

The general linear transformation with two fixed points is the product of a hyperbolic and an elliptic transformation with the same fixed points.

The fixed points of a linear transformation are found by solving the equation

z= .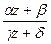

In general this is a quadratic equation with two roots; if γ =0, one of the fixed points is ∞. It may happen, however, that the roots coincide. A linear transformation with coinciding fixed points is said to be parabolic. The condition for this is (α -δ)²=4β γ.

*Source: L.Ahlfors Complex Analysis, p.31-33.