Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Problem solving
|
|
Can you prove the following propositions and explain how you obtained the results?
PROPOSITION 1.
Suppose that T1: Rn→ Rm and T2: Rm→ Rk are linear transformations. Then T=T2 ○ T1: Rn→ Rk is also a linear transformation.
PROPOSITION 2.
Suppose that the linear operator T: Rn→ Rn has standard matrix A. Then the following statements are equivalent:
(a) The matrix A is invertible.
(b) The linear operator T is one-to-one.
(c) The range of T is Rn, in other words, R(T) =Rn.
PROPOSITION 3.
A transformation T: Rn→ Rm is linear if and only if the following two conditions are satisfied:
(a) For every u, v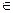 
Rn, we have T(u+v) =T(u) +T(v).
(b) For every u 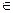Rn, and c 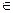R, we have T(cu) =cT(u).
*Source: WWL Chen, Linear Algebra. Chapter 8 Linear Transformations 2008.
https://rutherglen.science.mq.edu.au/wchen/lnlafolder/la08.pdf
Grammar Notes: