
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Text 1. A linear transformation between two vector spaces and is a map such that the following hold:
|
|
A linear transformation between two vector spaces 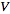 and
and 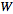 is a map
is a map 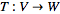 such that the following hold:
such that the following hold:
1.  for any vectors
for any vectors 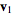 and
and 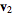 in
in 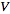 , and
, and
2. 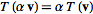 for any scalar
for any scalar 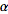 .
.
A linear transformation may or may not be injective or surjective. When 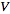 and
and 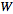 have the same dimension, it is possible for
have the same dimension, it is possible for  to be invertible, meaning there exists a
to be invertible, meaning there exists a 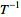 such that
such that 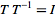 . It is always the case that
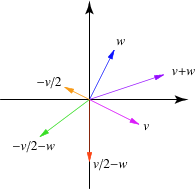
. It is always the case that 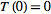 . Also, a linear transformation always maps lines to lines (or to zero).
. Also, a linear transformation always maps lines to lines (or to zero).
The main example of a linear transformation is given by matrix multiplication. Given an  matrix
matrix  , define
, define 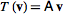 , where
, where 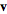 is written as a column vector (with
is written as a column vector (with 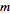 coordinates). For example, consider
coordinates). For example, consider

| (1) |
then  is a linear transformation from
is a linear transformation from  to
to  , defined by
, defined by
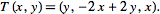
| (2) |
When 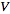 and
and 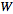 are finite dimensional, a general linear transformation can be written as a matrix multiplication only after specifying a vector space basis for
are finite dimensional, a general linear transformation can be written as a matrix multiplication only after specifying a vector space basis for 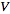 and
and 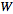 . When
. When 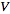 and
and 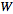 have an inner product, and their vector space bases,
have an inner product, and their vector space bases,  and
and 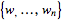 , are orthonormal, it is easy to write the corresponding matrix
, are orthonormal, it is easy to write the corresponding matrix 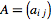 . In particular,
. In particular,  . Note that when using the standard basis for
. Note that when using the standard basis for 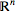 and
and 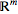 , the
, the 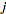 -th column corresponds to the image of the
-th column corresponds to the image of the 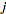 th standard basis vector.
th standard basis vector.
When 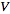 and
and 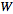 are infinite dimensional, then it is possible for a linear transformation to not be continuous. For example, let
are infinite dimensional, then it is possible for a linear transformation to not be continuous. For example, let 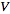 be the space of polynomials in one variable, and
be the space of polynomials in one variable, and  be the derivative. Then
be the derivative. Then 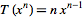 , which is not continuous because
, which is not continuous because  while
while 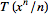 does not converge.
does not converge.
Linear two-dimensional transformations have a simple classification. Consider the two-dimensional linear transformation

| 
| 
| (3) |
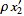
| 
| 
| (4) |
Now rescale by defining  and
and 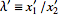 . Then the above equations become
. Then the above equations become
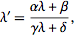
| (5) |
where  and
and 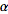 ,
,  ,
,  , and
, and 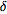 are defined in terms of the old constants. Solving for
are defined in terms of the old constants. Solving for  gives
gives

| (6) |
so the transformation is one-to-one. To find the fixed points of the transformation, set  to obtain
to obtain
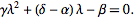
| (7) |
This gives two fixed points, which may be distinct or coincident. The fixed points are classified as follows.
| variables | type |

| hyperbolic fixed point |
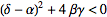
| elliptic fixed point |

| parabolic fixed point |
*Source: Rowland, Todd and Weisstein, Eric W. " Linear Transformation." From MathWorld --A Wolfram Web Resource. https://mathworld.wolfram.com/LinearTransformation.html