Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Euclidean Linear Transformations
|
|
By a transformation from Rn into Rm, we mean a function of the type T: Rn→ Rm, with domain Rn and codomain Rm. For every vector x 
Rn, the vector T(x) Rm is called the image of x under the transformation T, and the set
R(T) ={T(x): x Rn},
of all images under T, is called the range of the transformation T.
Remark.
For our convenience later, we have chosen to use R(T) instead of the usual T(Rn) to denote the range of the transformation T.
For every x= (x1 …, xn) Rn, we can write T(x) =T(x1 , …, xn) = (y1 , …, ym). Here, for every i= 1, …, m, we have
yi=Ti(x1, …, xn), (1)
where Ti: Rn→ R is a real valued function.
Definition.
A transformation T: Rn→ Rm is called a linear transformation if there exists a real
matrix A=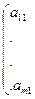 
… 
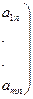
such that for every x= (x1, …, xn) Rn, we have T(x1, …, xn) = (y1, …, ym), where
y1=a11x1+… +a1nxn;
.
.
.
ym=am1x1+…+amnxn; (2)
which can also be written in matrix notation.
The matrix A is called the standard matrix for the linear transformation T.
Remarks.
(1) In other words, a transformation T: Rn→ Rm is linear if the equation (1) for every
i = 1, …, m is linear.
(2) If we write x Rn and y Rm as column matrices, then (2) can be written in the form y=Ax, and so the linear transformation T can be interpreted as multiplication of x Rn by the standard matrix A.
Definition.
A linear transformation T: Rn→ Rm is said to be a linear operator if n=m. In this case, we say that T is a linear operator on Rn.
Example 8.1.1.
The linear transformation T: R5→ R3, defined by the equations
y1= 2x1+3x2+5x3+7x4-9x5,
y2= 3x2+4x3 +2x5,
y3= x1 +3x3-2x4,
can be expressed in matrix form as
.
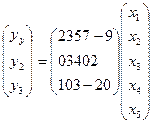If (x1 , x2, x3, x4, x5) = (1, 0, 1, 0, 1), then
,
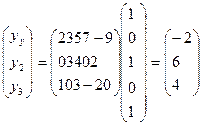so that T(1, 0, 1, 0, 1)=(-2, 6, 4).
Example 8.1.2.
Suppose that A is the zero m x n matrix. The linear transformation T: Rn→ Rm,
where T(x) =Ax for every x Rn, is the zero transformation from Rn into Rm. Clearly T (x) =0 for every x Rn.
Example 8.1.3.
Suppose that I is the identity n x n matrix. The linear operator T: Rn→ Rn, where T(x) = I x for every x Rn, is the identity operator on Rn. Clearly T(x) = x for every
x Rn.
PROPOSITION 8A.
Suppose that T: Rn→ Rm is a linear transformation, and that {e1, …, en} is the standard basis for Rn.. Then the standard matrix for T is given by A=(T(e1), …, T(en)), where T(ej) is a column matrix for every j = 1, …, n.
Proof.
This follows immediately from (2).