Предприятие и рынок в коротком периоде

В теории рынков понятия периодов несколько уточняются. Мы можем дать им следующие определения.

Мгновенным периодом называется столь короткий период, что выпуск каждого предприятия и количество предприятий в отрасли фиксировано.

Коротким периодом называется такой период, в течение ко­торого производственные мощности каждого предприятия (раз­меры и число заводов, фабрик, других производственных еди­ниц) фиксированы, но выпуск может быть увеличен или снижен за счет изменения объема использования переменных факторов. Общее число предприятий в отрасли остается неизменным.

Длительным периодом называют такой период, в течение которого производственные мощности могут быть приспособле­ны к условиям спроса и затрат. В предельном случае (если ус­ловия деятельности совершенно неблагоприятны) предприятие может полностью прекратить деятельность (уйти из отрасли или с рынка). С другой стороны, новые предприятия могут войти в отрасль (на рынок) в случае благоприятных рыночных усло­вий. Таким образом, число предприятий в однородной отрасли в длительном периоде может варьировать.

В условиях совершенной конкуренции предприятие является ценополучателем. Оно может максимизировать свою прибыль, лишь приспособив объем выпуска к условиям товарного рын­ка, с одной стороны, и/или к обусловленным технологией соб­ственным затратам — с другой. Но оно не может оказать вли­яние на цену продукции. Определим выпуск, обеспечивающий максимум прибыли совершенно конкурентного предприятия при заданных условиях рынка и технологии. Заметим лишь предварительно, что экономисты называют максимумом при­были как максимум положительной разницы между выруч­кой и затратами производства продукции, так и минимум от­рицательной разности между теми же величинами. Поэтому минимум убытков может рассматриваться как максимум при­были, если получить положительную прибыль невозможно.

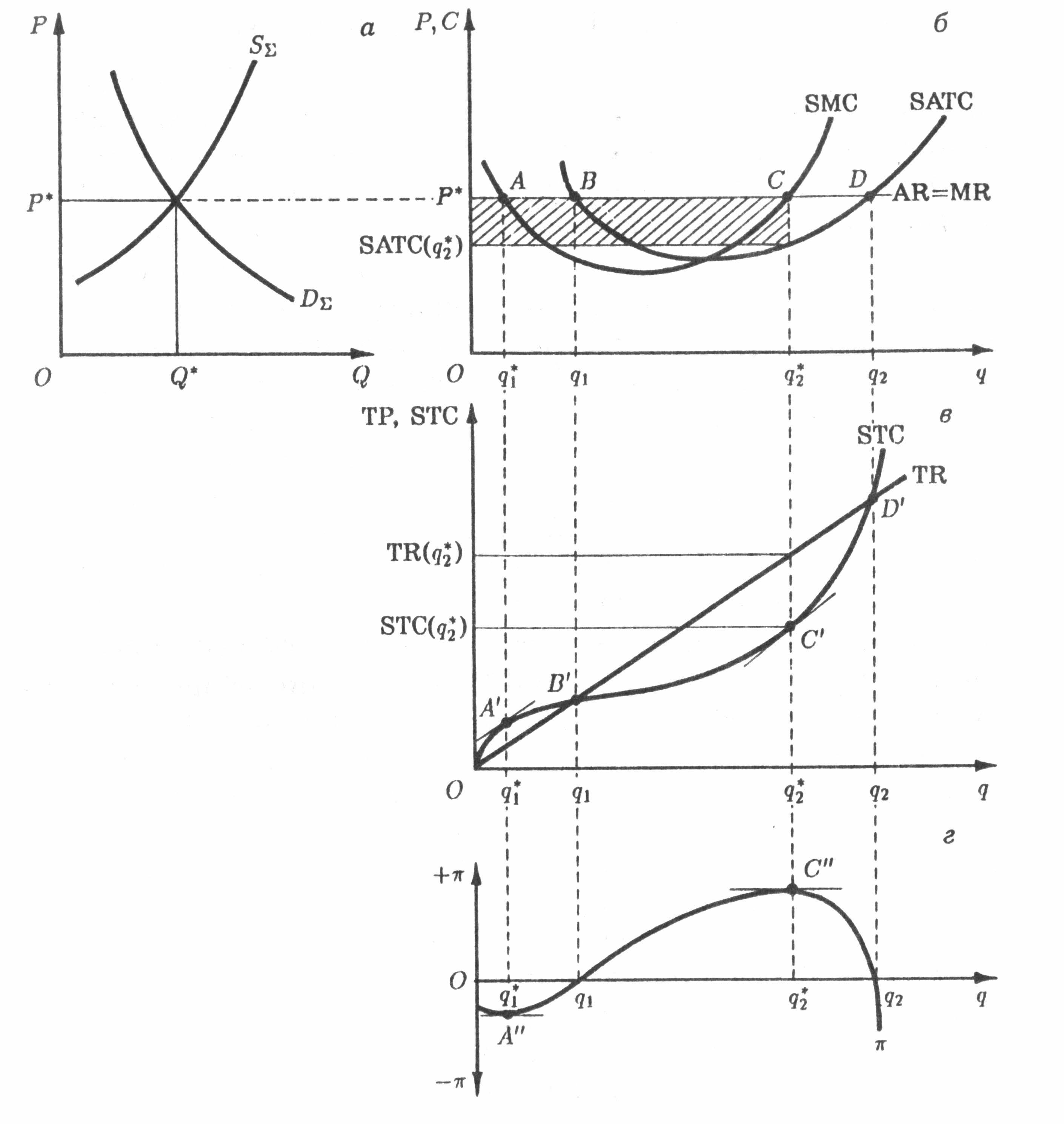
Пусть условия товарного рынка таковы, как показано на рис. 4.2, а, где D_∑ и S_∑ — рыночные кривые спроса и предложе­ния; Р* и Q* — соответственно рыночная цена равновесия и рав­новесный объем выпуска (продаж) отрасли в единицу времени. Пусть, далее, кривые SMC, SATC и STC на рис. 4.2, б, в представ­ляют кривые предельных, средних общих и общих затрат типич­ного предприятия в коротком периоде. Поскольку предприятие является ценополучателем, линия AR = MR на рис. 4.2, б явля­ется линией спроса на продукцию предприятия, тогда как луч TR на рис. 4.2, в — линия его общей выручки. Наклон линии TR неизменен на всем ее протяжении, поскольку цена не зависит от объема выпуска данного предприятия, и потому TR = P*q.

Прибыль предприятия представляет разность между общей выручкой и общими затратами короткого периода:

π (q) = TR(q) – STC(q).

Условием максимизации прибыли первого порядка (необ­ходимым) будет, очевидно, а поскольку dTR(q}/dq = MR(q) и dSTC(q}/dq =MC(q),

услови­ем первого порядка является равенство предельной выручки предельным затратам:

MR(g*)=MC(g*)

Но для совершенно конкурентного предприятия Р ≡ AR = MR, и, следовательно, условие первого порядка может быть пред­ставлено и как равенство предельных затрат цене:

МС(q*)=Р

В ситуации, представленной на рис. 4.2, б, условие первого порядка выполняется дважды, в точках А и С, которым соот­ветствуют объемы выпуска q₁* и q₂*. Однако, как видно на рис. 4.2, г, в первом случае максимальны убытки, во втором — прибыль. Для различения этих случаев

используется условие второго порядка (достаточное):

Левая часть характеризует наклон кривой MR, правая — наклон кривой SMC. Следовательно, условие второго поряд­ка требует, чтобы наклон кривой предельных затрат был больше наклона кривой предельной выручки, или, иначе, что­бы кривая SMC пересекала кривую MR снизу (как в точке С, но не в А на рис. 4.2, б).

Поскольку же для совершенно конкурентного предпри­ятия цена не зависит от объема выпуска, наклон кривой пре­дельной выручки

условие второго порядка можно представить неравенством

Последнее означает, что прибыль будет максимальна, если в точке пересечения с MR кривая SMC имеет положительный наклон.

Другими словами, прибыль (положительная) будет мак­симальна, если MR = SMC и кривая SMC восходящая. На­против, отрицательная прибыль (убытки) будет максималь­на, если MR = SMC и кривая SMC нисходящая. На рис. 4.2, б максимальная положительная прибыль при выпуске q₂* со­ответствует площади заштрихованного прямоугольника.

Условие первого порядка можно переформулировать и таким образом: общая прибыль максимальна при таком объе­ме выпуска, когда предельная прибыль равна нулю. Предель­ной прибылью называют прирост прибыли в результате изменения объема выпуска на одну единицу продукции, т. е.

Mπ (q) = MR(q)- SMC(q)

или, в непрерывном случае,

Геометрически предельная прибыль характеризуется наклоном кривой прибыли при определенном выпуске (q). Когда прибыль достигает максимума, наклон ее кривой становится нулевым. Так, в точках А» и С» на рис. 4.2, г касательные к кривой прибыли π имеют нулевой наклон:

M π (q₁*) = 0, Mπ (q₂*) = 0

Отметим также две точки переломного уровня вы­пуска (англ. break-even level): q₁ и q₂. Это точки безубыточного (или бесприбыльного) выпуска. Заметим, что в соответствую­щихим на рис. 4.2, б точках В и D AR = MR = SATC, а в точ­ках В' и D’ на рис. 4.2, б TR = STC. Наконец, на рис. 4.2, г точки q₁ и q₂ соответствуют нулевой прибыли.

Таким образом, рост выпуска от 0 до q₁* сопровождается ростом отрицательной прибыли (убытков). В дальнейшем убытки сокращаются, а достигнув выпуска q₁ предприятие начинает получать все возрастающую (вплоть до q₂*) прибыль. Дальней­ший рост выпуска будет сопровождаться снижающимся рос­том прибыли. Наконец, увеличение выпуска сверх точки вто­рого перелома (q₂) вновь сделает предприятие убыточным (SATC> P=AR=MR).

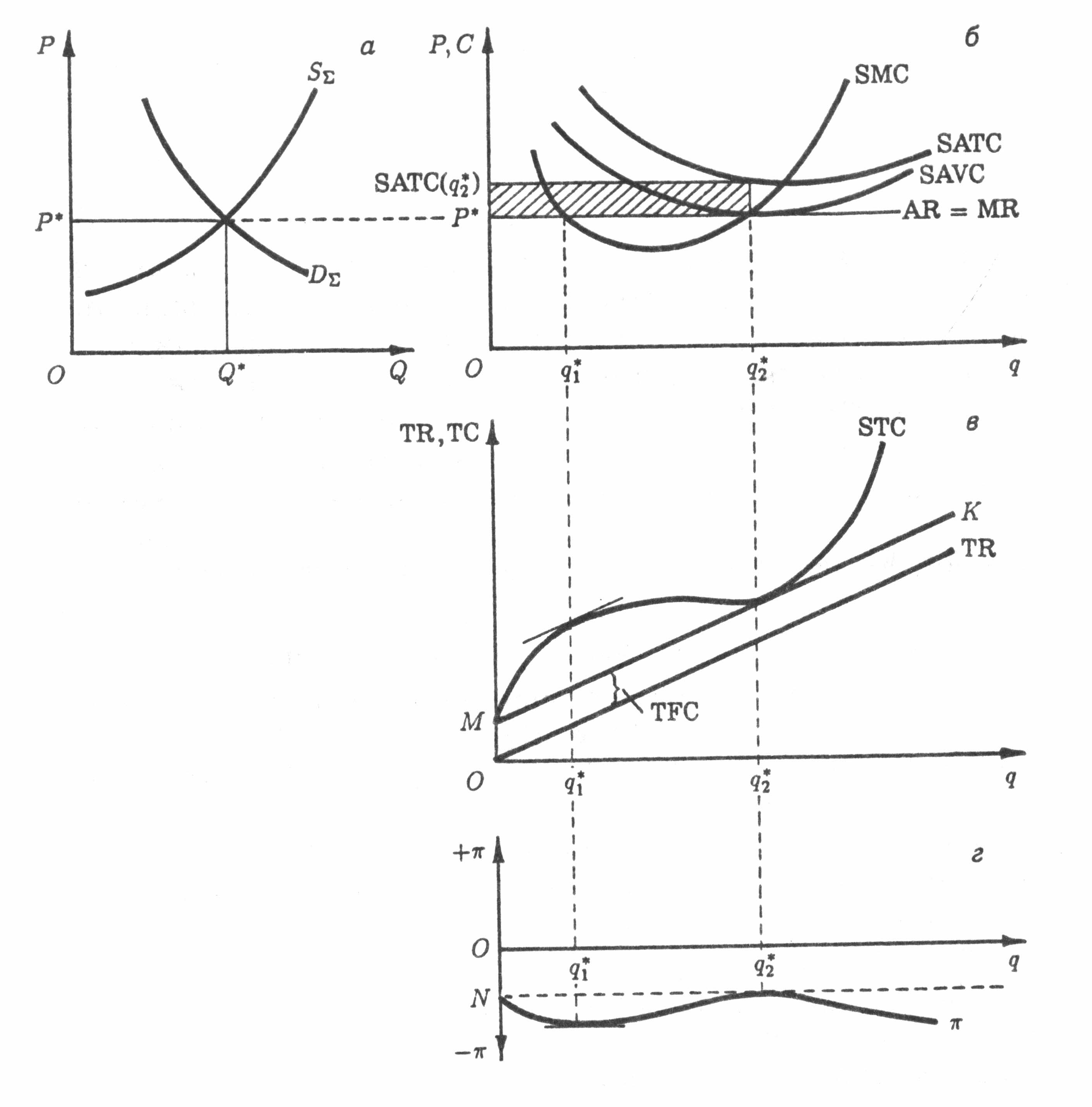На рис. 4.3 представлена ситуация, в которой предприятию безразлично, выпускать ли продукцию в объеме q₂* или закрыть­ся. Рыночная цена продукции (наклон луча TR на рис. 4.3, в) равна минимуму средних переменных затрат предприятия (ли­ния AR=MR на рис. 4.3, б касается кривой SAVC в точке минимума последней). При таком уровне цены, как следует из рис. 4.3, г, максимум прибыли, π =|ON|, одинаков и при вы­пуске q₂*, и при нулевом выпуске. При этом |ON| в точности равен сумме постоянных затрат (ОМ на рис. 4.3, в). Таким обра­зом, ясно, что и при нулевом выпуске, и при производстве про­дукции в объеме q₂* предприятие получит убытки, равные об­щим постоянным затратам. При любом другом объеме произ­водства сумма (отрицательной) прибыли, как следует из рис. 4.3, г, будет выше.

4 Предложение совершенно конкурентной отрасли в коротком периоде

Предложение совершенно конкурентного предприятия в коротком периоде.

Функцией предложения о цены называют зависимость величины предложения от данного товара. Можно показать, что кривая предложения совершенно конкурентного предприятия в коротком периоде тождественна части его кривой предельных затрат.

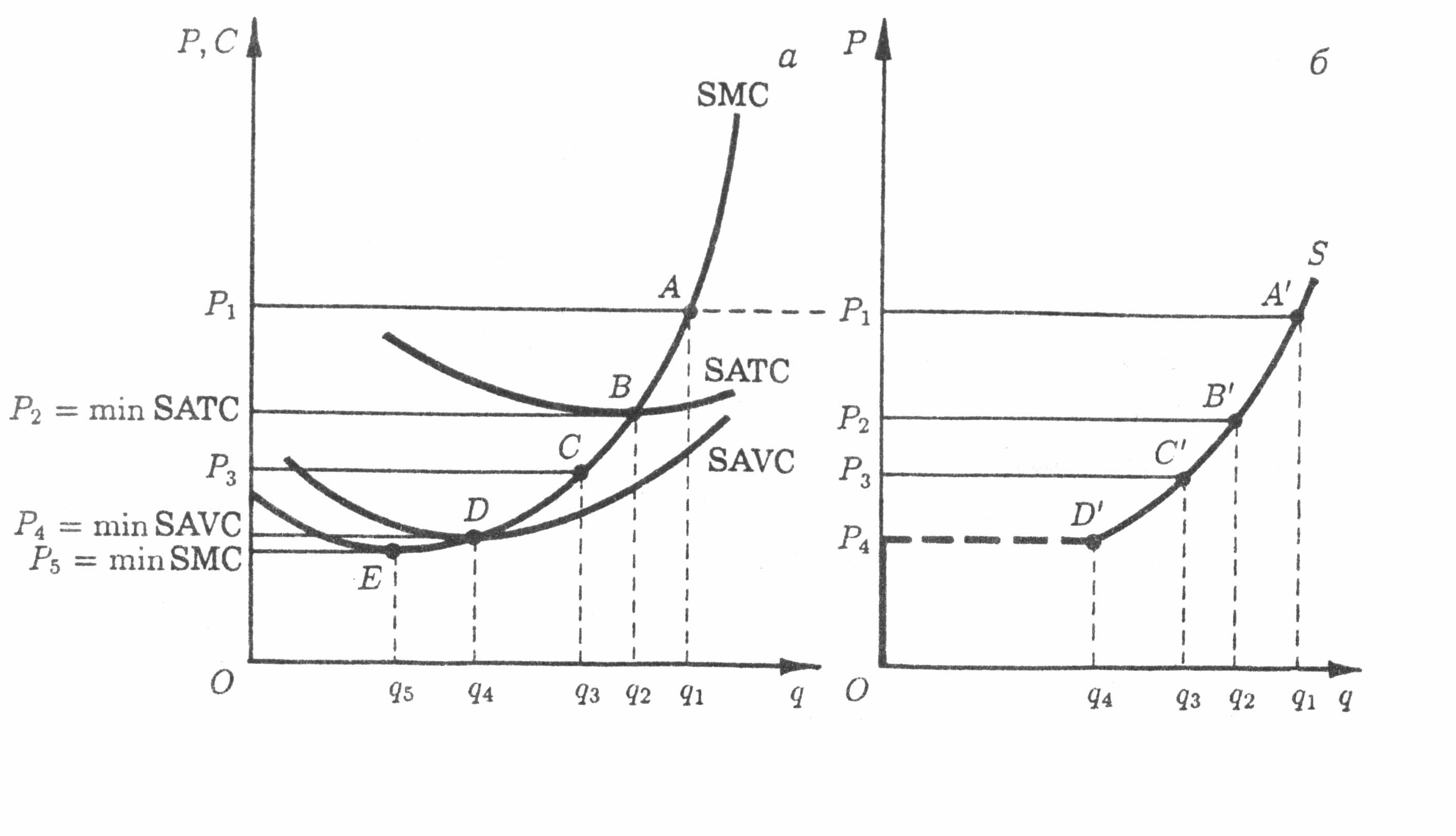
На рис. 4.4, а представлены кривые предельных (SMC). Средних общих (SATC) и средних переменных (SAVC) затрат. При цене Р₁ максимум положительной прибыли достигается при выпуске q₁; значит, точка А на кривой SMC принадлежит кривой предложения данного прибылемаксимизирующего пред­приятия. При более низкой цене, Р₂, прибыль будет макси­мальна при выпуске q₂; значит, и точка В на кривой SMC при­надлежит кривой предложения. Заметим, что в этом случае мак­симум (положительной) прибыли равен нулю, поскольку цена Р₂ равна минимуму средних общих затрат (Р₂ = AR = MR = minSATC).

Но, с другой стороны, Р₃ > SAVC(q₃). А это значит, что выруч­ка от продажи выпуска q₃ возместит все переменные и, кро­ме того, часть постоянных затрат предприятия. Таким обра­зом, убытки от выпуска q₃ будут меньше, чем сумма общих постоянных затрат (TFC) в коротком периоде. Поэтому по сравнению с нулевым выпуском выпуск q₃ будет прибылемаксимизирующим. Следовательно, и точка С принадлежит кривой предложения предприятия.

При еще более низкой цене Р₄ = minSAVC выпуск q₄ удов­летворяет обоим условиям максимизации прибыли. Это зна­чит, что TR(q₄) = q₄ (SAV C(q₄)) = TVC(q₄) и, следовательно, убыт­ки предприятия равны сумме постоянных затрат. В этих усло­виях предприятию безразлично, производить ли q₄ единиц про­дукции или закрыться. Поэтому точку D на

кривой SMC часто называют точкой закрытия {англ. schutdown point). Эта точка может принадлежать кривой предложения предприятия, а может и не принадлежать.

Наконец, при цене P₅ = minSMC выпуск q₅ также удов­летворяет условиям максимизации, но цена не возмещает средних переменных затрат ( P₅ < SAVC(q₅)), и при любом от­личном от нуля выпуске убытки окажутся выше постоян­ных затрат. Следовательно, в этом случае нулевой выпуск окажется оптимальным. Иначе говоря, при Р < minSAVC прибылемаксимизирующее предприятие предпочтет за­крыться, Поэтому точка Е на кривой SMC определенно не принадлежит кривой предложения совершенно конкурент­ного предприятия.

Кривая предложения совершенно конкурентного предпри­ятия представлена на рис. 4.4, б. Здесь точки А', В', С', D' соответствуют точкам А, В, С, D кривой SMC на рис. 4.4, а. Множество подобных точек формирует участок кривой пред­ложения, лежащий выше точки D', соответствующей миниму­му SAVC на рис. 4.4, а. Заметим, что участок кривой SMC, лежащий ниже SAVC, не входит в кривую предложения, по­скольку прибылемаксимизирующее поведение диктует закры­тие предприятия, если цена продукции окажется ниже сред­них переменных затрат.

Таким образом, кривая предложения совершенно конку­рентного предприятия в коротком периоде представляет собой возрастающую ветвь кривой предельных затрат, ко­торая лежит выше минимума средних переменных затрат. При более низком, чем minSAVC, уровне рыночной цены кри­вая предложения сливается с осью цен (участок ОР₄ на рис.4.4, 6).