
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Рівняння Такагі. Рівняння для повільно змінних амплітуд поля.
|
|
Розглянемо перехід від хвильового рівняння (1.13) до системи рівнянь для повільно змінних амплітуд поля у випадку дифракції на ідеальному кристалі. Поляризуємість 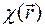 ідеального кристалу є трьохмірною періодичною функцією (скінченність розмірів кристалу в цьому випадку до уваги не береться):
ідеального кристалу є трьохмірною періодичною функцією (скінченність розмірів кристалу в цьому випадку до уваги не береться):
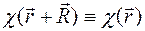 ,
,
де 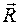 - довільний вектор трансляції кристалічної гратки. Значить, поляризуємість
- довільний вектор трансляції кристалічної гратки. Значить, поляризуємість 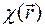 можна розкласти в ряд Фур’є за векторами оберненої гратки
можна розкласти в ряд Фур’є за векторами оберненої гратки 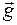
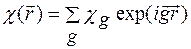 . (1.14)
. (1.14)
Вважатимемо, що вектор 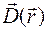 в (1.13) можна представити у вигляді розкладу за хвилями із залежними від координат амплітудами
в (1.13) можна представити у вигляді розкладу за хвилями із залежними від координат амплітудами 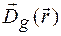 :
:
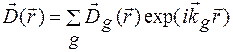 , (1.15)
, (1.15)
де 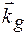 - хвильові вектори дифракційних хвиль в кристалі, які ми визначимо без врахування ефектів заломлення і взаємодії хвиль в кристалі згідно умови дифракції у вакуумі:
- хвильові вектори дифракційних хвиль в кристалі, які ми визначимо без врахування ефектів заломлення і взаємодії хвиль в кристалі згідно умови дифракції у вакуумі:
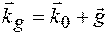 ,
, 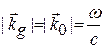 . (1.16)
. (1.16)
Тоді ефекти заломлення і взаємодії хвиль в кристалі повинні відобразитися в амплітудах 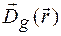 . Умову дифракції (1.16) можна переписати у вигляді умови сингулярності розсіяних хвиль в координатному просторі, тоді воно приймає вигляд закону Вульфа-Брега
. Умову дифракції (1.16) можна переписати у вигляді умови сингулярності розсіяних хвиль в координатному просторі, тоді воно приймає вигляд закону Вульфа-Брега
2dsinq=nl,
де d-період гратки вздовж вектору дифракції, q-кут Брега, n-порядок відбивання, l-довжина хвилі.

Рис.1. Геометричне представлення ідеалізованих умов фазового синхронізму хвиль (умови дифракції) у кристалі в просторі хвильових векторів. Штрихова лінія –умовний показ однієї з атомних площин.
Вважатимемо, що амплітуди 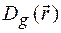 міняються повільно в порівнянні з фазовими складовими exp(
міняються повільно в порівнянні з фазовими складовими exp(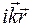 ) в (1.15). Підставимо (1.14) і (1.15) у рівняння (1.13) виконуючи відповідно певні операції. В результаті отримаємо
) в (1.15). Підставимо (1.14) і (1.15) у рівняння (1.13) виконуючи відповідно певні операції. В результаті отримаємо
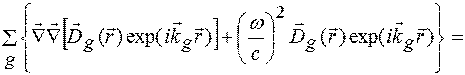
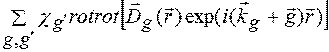 . (1.17)
. (1.17)
Розглянемо першу складову в лівій частині рівняння (1.17)
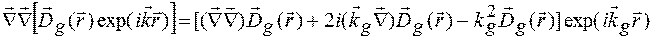
Оскільки ми вважаємо, що 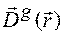 є повільно змінними у порівнянні з
є повільно змінними у порівнянні з 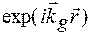 , то має місце нерівність
, то має місце нерівність 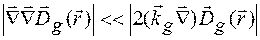 .
.
Це дає змогу в лівій частині рівняння (1.17) знехтувати складовими, що містять другі похідні по 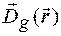 , в результаті ліва частина (1.17) прийме вигляд
, в результаті ліва частина (1.17) прийме вигляд
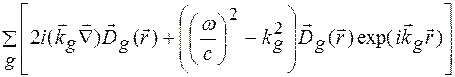 (1.18)
(1.18)
Таким же чином в правій частині рівняння (1.17) всі складові, що місять другі похідні 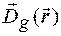 , котрі з’являються в результаті дії оператора rotrot, можна одразу опустити. Крім того, оскільки в правій частині знаходиться множник
, котрі з’являються в результаті дії оператора rotrot, можна одразу опустити. Крім того, оскільки в правій частині знаходиться множник 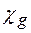 , то можна опустити і всі складові з першими похідними
, то можна опустити і всі складові з першими похідними 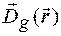 , оскільки ці складові дають лише малу добавку (порядка
, оскільки ці складові дають лише малу добавку (порядка 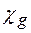 ) до перших похідних
) до перших похідних 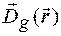 в лівій частині.
в лівій частині.
Отже, залишається подіяти оператором rotrot лише на експоненціальні множники в правій частині (1.17), що дає наступний результат:

Згідно з (1.16) 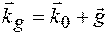 і
і 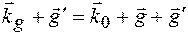 . Введемо позначення
. Введемо позначення 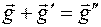 , і оскільки сума векторів оберненої гратки є також є вектором оберненої гратки, заміняємо подвійну суму по h i h¢ подвійною сумою по h i h². Така заміна можлива завжди, оскільки сумування ведеться по всім векторам оберненої гратки. В результаті отримаємо:
, і оскільки сума векторів оберненої гратки є також є вектором оберненої гратки, заміняємо подвійну суму по h i h¢ подвійною сумою по h i h². Така заміна можлива завжди, оскільки сумування ведеться по всім векторам оберненої гратки. В результаті отримаємо:
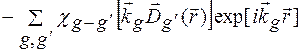 (1.19)
(1.19)
Для зручності співставлення цього виразу з (1.18) зробимо наступні перепозначення: h®h¢ і h² ®h.
Прирівнюючи (1.18) і (1.19) відзначимо. що ці суми можуть бути рівні тільки тоді, коли рівні коефіцієнти при однакових експонентах, отримуємо наступну безмежну систему диференціальних рівнянь в частинних похідних першого порядку:
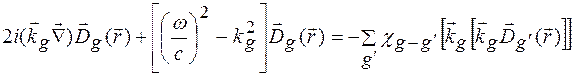 (1.20)
(1.20)
Подвійний векторний добуток у правій частині системи рівнянь (1.20) проектує вектор поляризації поля 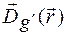 на напрямок, перпендикулярний хвильовому вектору
на напрямок, перпендикулярний хвильовому вектору 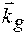 .
.
Система рівнянь (1.20) описує розповсюдження в кристалі безмежного числа зв’язаних між собою дифракційних хвиль і загальне рівняння цієї системи є не менш складною задачею я і рішення вихідного рівняння (1.13).