
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Двохвильова дифракція в одномірно спотвореному кристалі.
|
|
Розглянемо вивід рівнянь для повільно змінних амплітуд (рівнянь Такагі) для кристалу з одномірним полем спотворень. При цьому ми обмежимось лише одним важливим в практичному значенні типом спотворення, коли атомні площини зміщені відносно положень в ідеальному кристалі без зміни їх розсіючої здатності. Ця модель охоплює широкий круг об’єктів, до яких належать іонно-імплантовані і дифузійні шари, епітаксійні плівки, надгратки та ін. В рамках цієї моделі вважатимемо, що поляризуємість кристалу 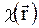 не відрізняється поляризуємості ідеального кристалу і тому може бути розкладена в ряд Фур’є (1.14). Вектор електричного зміщення
не відрізняється поляризуємості ідеального кристалу і тому може бути розкладена в ряд Фур’є (1.14). Вектор електричного зміщення 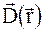 розкладемо в ряд по повільно змінним амплітудам
розкладемо в ряд по повільно змінним амплітудам 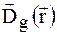 :
:
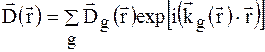 , (1.28)
, (1.28)
де на відміну від (1.15) хвильовий вектор 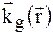 – функція координат в кристалі. Оскільки спотворення в кристалі зводяться за допущенням до зміщення атомів, тобто до зміни фаз розсіяних хвиль в порівнянні з ідеальною граткою, то показник експоненти в (1.28) має вигляд
– функція координат в кристалі. Оскільки спотворення в кристалі зводяться за допущенням до зміщення атомів, тобто до зміни фаз розсіяних хвиль в порівнянні з ідеальною граткою, то показник експоненти в (1.28) має вигляд
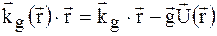 (1.29)
(1.29)
де 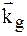 – хвильовий вектор поля в ідеальному кристалі, а
– хвильовий вектор поля в ідеальному кристалі, а 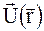 – функція, що задає поле зміщень. Вважатимемо, що поле зміщень змінюється повільно в порівнянні з величиною постійної гратки, а самі зміщення малі. Складова
– функція, що задає поле зміщень. Вважатимемо, що поле зміщень змінюється повільно в порівнянні з величиною постійної гратки, а самі зміщення малі. Складова 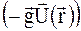 в правій частині (1.29) описує додаткові фазові зсуви розсіяних хвиль відносно їх положень в ідеальній кристалічній гратці. Діючи оператором градієнта на обидві частини (1.29), отримаємо вирази для хвильових векторів в спотвореному кристалі:
в правій частині (1.29) описує додаткові фазові зсуви розсіяних хвиль відносно їх положень в ідеальній кристалічній гратці. Діючи оператором градієнта на обидві частини (1.29), отримаємо вирази для хвильових векторів в спотвореному кристалі:
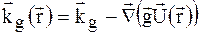 (1.30а)
(1.30а)
або, з врахуванням умови (1.16):
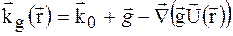 (1.30б)
(1.30б)
Цей результат можна трактувати як визначення локального вектору оберненої гратки 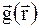 спотвореного кристалу:
спотвореного кристалу:
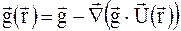 (1.31)
(1.31)
Для рішення рівняння (1.13) підставимо в нього розклади (1.14) і (1.28). Підстановка розкладу (1.28) для 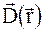 в ліву частину (1.13) приведе до наступного результату:
в ліву частину (1.13) приведе до наступного результату:
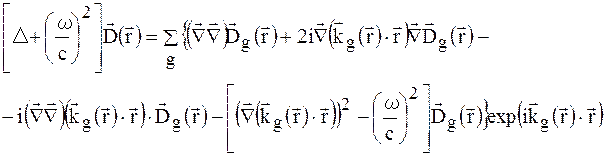 (1.32)
(1.32)
де 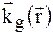 визначається співвідношенням (1.30). Враховуючи, що за допущенням амплітуди
визначається співвідношенням (1.30). Враховуючи, що за допущенням амплітуди 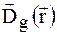 і хвильові вектори
і хвильові вектори 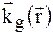 змінюються повільно в порівнянні з фазовими складовими, перша і третя складові по сумі g в правій частині (1.32) можна опустити. Розглянемо другу складову під знаком суми в (1.32):
змінюються повільно в порівнянні з фазовими складовими, перша і третя складові по сумі g в правій частині (1.32) можна опустити. Розглянемо другу складову під знаком суми в (1.32):
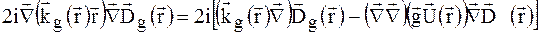
Другий член в квадратних дужках в правій частині цього рівняння містить другі похідні від повільно змінної функції зміщення 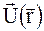 і може бути також опущеним. Першу складову в квадратних дужках використовуючи (1.30а) перепишемо у вигляді:
і може бути також опущеним. Першу складову в квадратних дужках використовуючи (1.30а) перепишемо у вигляді:
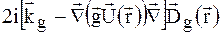 .
.
Очевидно, що складовою пропорційною 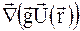 можна знехтувати. В результаті отримаємо
можна знехтувати. В результаті отримаємо
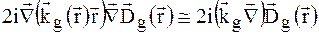 (1.33)
(1.33)
Повернемось тепер до розгляду четвертої складової в правій частині (1.32)
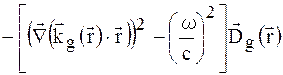 .
.
На основі результатів (1.30а), (1.22) і (1.23) перший член в квадратних дужках перепишемо у вигляді:
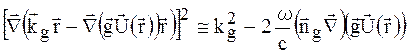 (1.34)
(1.34)
де 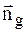 - одиничний вектор вздовж
- одиничний вектор вздовж 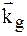 . Враховуючи (1.33), (1.34), праву частину (1.32) (тобто, відповідно, ліву частину рівняння (1.13)) можна представити у вигляді:
. Враховуючи (1.33), (1.34), праву частину (1.32) (тобто, відповідно, ліву частину рівняння (1.13)) можна представити у вигляді:
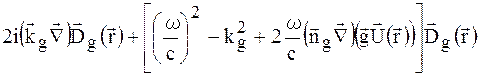 (1.35)
(1.35)
Розглянемо тепер праву частину рівняння (1.13), яка має наступний вигляд 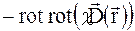 . Підставимо в цей вираз розклади (1.14), (1.28) і врахуємо, що величини домножуються на малі множники
. Підставимо в цей вираз розклади (1.14), (1.28) і врахуємо, що величини домножуються на малі множники 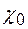 ,
, 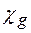 . Тоді, опускаючи всі складові, що містять любі похідні амплітуд
. Тоді, опускаючи всі складові, що містять любі похідні амплітуд 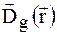 і функції зміщення
і функції зміщення 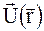 , після дії оператора rotrot на експоненту (в подвійному векторному добутку вектор
, після дії оператора rotrot на експоненту (в подвійному векторному добутку вектор 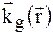 слідує замінити вектором
слідує замінити вектором  отримаємо
отримаємо
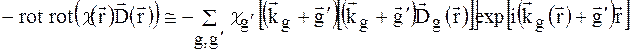 .
.
Перетворимо подвійну суму по g і g` так, як це було зроблено при виводі (1.19), найдемо
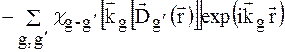 (1.36)
(1.36)
Прирівнюючи (1.35) і (1.36), знову отримаємо безмежну систему диференціальних рівнянь першого порядку для повільно змінних амплітуд поля 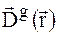 в кристалі із спотвореннями:
в кристалі із спотвореннями:
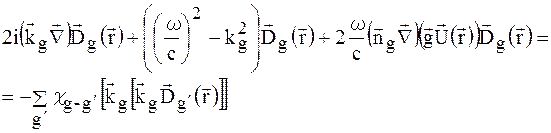 (1.37)
(1.37)
У відповідності з визначенням хвильових векторів розсіяних хвиль 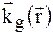 (1.30) в спотвореному кристалі і умов (1.22), (1.23) введемо в лівій частині системи (1.37) поняття локальної акомодації
(1.30) в спотвореному кристалі і умов (1.22), (1.23) введемо в лівій частині системи (1.37) поняття локальної акомодації 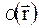 :
:
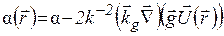 (1.37¢)
(1.37¢)
Дещо пізніше розглянемо двопроменеву дифракцію плоскої хвилі в кристалі при умові, що функція зміщень 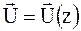 , тобто залежить лише від координати z. Тоді із всієї системи рівнянь (1.37) слід зберегти лише два рівняння, в результаті чого вона приймає вигляд:
, тобто залежить лише від координати z. Тоді із всієї системи рівнянь (1.37) слід зберегти лише два рівняння, в результаті чого вона приймає вигляд:
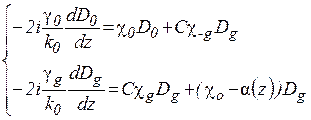 (1.38)
(1.38)
Відмінність системи рівнянь (1.38) від системи (1.25), яка описує дифракцію на ідеальному кристалі, полягає в тому, що акомодація a (1.22) замінюється на локальну акомодацію a(z). Для одновимірного поля спотворень 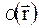 залежить лише від координати z.
залежить лише від координати z.
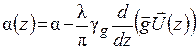 (1.39)
(1.39)
Виконаємо в системі рівнянь (1.38) експоненціальне перетворення 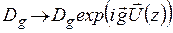 тоді система (1.38) прийме вигляд:
тоді система (1.38) прийме вигляд:
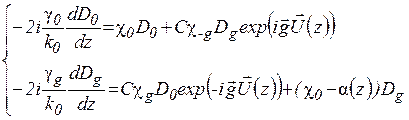 (1.40)
(1.40)
Система рівнянь (1.40) допускає наступну інтерпретацію: в кожній точці z кристалу дифракційне (складова 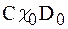 ) і дворазово розсіяне (складова
) і дворазово розсіяне (складова 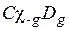 ) поля отримують додаткові, в порівнянні з ідеальним кристалом, зсуви фаз
) поля отримують додаткові, в порівнянні з ідеальним кристалом, зсуви фаз 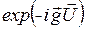 і
і 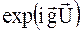 , відповідно. При цьому кристал розглядається як досконалий і вводиться незалежна від координат акомодація (1.22). Відзначимо, що систему (1.40) можна отримати формально заміною
, відповідно. При цьому кристал розглядається як досконалий і вводиться незалежна від координат акомодація (1.22). Відзначимо, що систему (1.40) можна отримати формально заміною 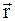 в розкладі (1.14) на
в розкладі (1.14) на 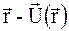 . При цьому для амплітуди поля
. При цьому для амплітуди поля 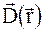 використовується розклад (1.15).
використовується розклад (1.15).