
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение графиков
|
|
Современные версии пакета MathCad обладают мощными графическими возможностями. В частности они позволяют строить графики различных типов в двумерных системах координат, а также трехмерные графики. Примеры построения графиков различных типов, а также решение других задач можно просмотреть в демонстрационных файлах (папка qsheet).
Инструменты для построения графиков в MathCad доступны в меню Insert è Graph или в палитре операторов. На этой палитре расположены все основные типы графиков:
· график кривой в двумерной декартовой системе координат (X-Y Plot);
· график кривой в полярной системе координат (Polar Plot);
· поверхность (Surface);
· столбиковая трехмерная (3D) диаграмма (3D Bar Plot);
· точечный трехмерный (3D) график (3D Scatter Plot).
Двумерный декартов график (кнопка X-Y Plot) – самый распространенный график. Он иллюстрирует связи между двумя или несколькими векторами. Графическая область представляет собой две вложенные рамки. Во внутренней отображаются непосредственно кривые зависимости. Пространство между рамками служит для визуализации разного рода служебной информации. Графическую область можно увеличивать и уменьшать с помощью специальных маркеров, расположенных на ее внешней рамке.
MathCad допускает различную детализацию при описании характеристик графика. Можно выделить два варианта такой детализации.
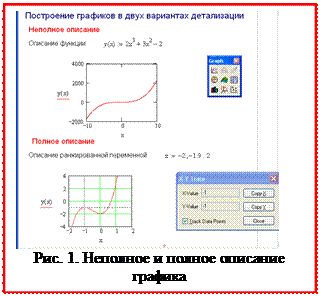
1. Неполное описание соответствует такой ситуации, когда задается только вид функции, график которой нужно построить, а пределы, шаг изменения графика, масштаб и формат задаются автоматически (рис. 10).
2. Полное описание соответствует такой ситуации, когда кроме вида функции явно описываются пределы изменения и шаг аргумента. Пределы изменения значений аргумента и функции указываются в соответствующих позициях шаблона (рис. 10).
 Рассмотрим данный вариант, разбив построение графика на три этапа.
Рассмотрим данный вариант, разбив построение графика на три этапа.
Этап 1: задание вида функций одной переменной.
Этап 2: формирование вектора значений аргумента. Механизм многократного повторения вычислений реализован в виде ранжированной переменной (рис. 11).
Этап 3: построение графика. Третий этап в свою очередь делится на три шага.
Шаг 1: вызов шаблона графика – прямоугольника с чёрными квадратиками у левой и правой сторон.
Шаг 2: заполнение пользователем пустых полей в середине вертикальной и горизонтальной осей именем функции и именем аргумента. Если функций больше одной, то их имена вводятся через запятую.
Шаг 3: другие четыре пустых поля (предельные значения аргумента и функции) среда заполняет сама в случае неполного описания. В случае полного описания эти поля заполняет пользователь.
График появляется на дисплее после вывода курсора из зоны графика, (рис. 10). На рисунке видно, что вариант полного описания графика позволяет выявить все особенности функции: экстремумы, точки пересечения с осями координат.
 Окно форматирования вида графической области Format, открыть которое можно с помощью одноименной команды контекстного меню, позволяет установить параметры графика.
Окно форматирования вида графической области Format, открыть которое можно с помощью одноименной команды контекстного меню, позволяет установить параметры графика.
Для управления отображением линий на графике существует вкладка Traces, где приведен формат каждой линии и элементы управления изменением формата. Маркеры для отдельных точек можно выбрать из списка Symbol, из списка Lіne выбирается тип линии, а из списка Color − цвет графика. Список Type определяет средство связи отдельных точек графика, а список Weіght − толщину линии на графике.
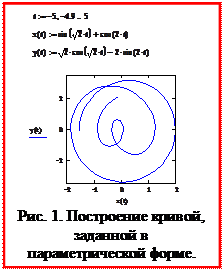
Графики функций, заданных в параметрической форме, строятся аналогично. Отличие состоит в том, что в позициях аргумента и функции вводятся выражения или имена соответствующих функций параметра (рис. 11).
Варианты заданий
1. Построить график функции в двух вариантах детализации: неполное описание и полное описание. На графике с полным описанием нанести линии сетки и заголовки.
Составить таблицы значений аргумента и функции. Сопроводить задачу краткими пояснениями.
| Вариант | Функция y(x) | Вариант | Функция y(x) |
 y= y= 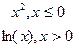
| 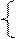 y= y= 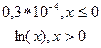
| ||
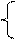 y= y= 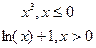
| 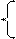 y= y= 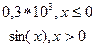
| ||
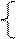 y= y= 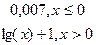
|  y= y= 
| ||
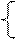 y= y= 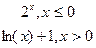
| 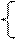 y= y= 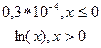
| ||
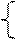 y= y= 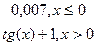
|  y= y= 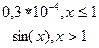
| ||
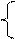 y= y= 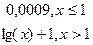
| 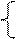 y= y= 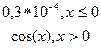
| ||
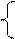 y= y= 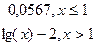
| 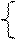 y= y= 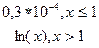
| ||
 y= y= 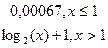
| 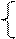 y= y= 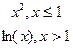
| ||
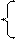 y= y= 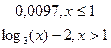
|  y= y= 
| ||
 y= y= 
|  y= y= 
| ||
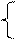 y= y= 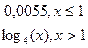
| 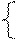 y= y= 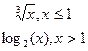
| ||
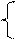 y= y= 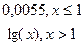
| 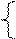 y= y= 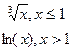
|
2. Построить график функции, заданной в параметрическом виде.
| Вариант | Функция | Вариант | Функция |
| x= 2 cos t y = sin t | x= sin t - cos 2t y = cos t | ||
| x= 2 cos3 t y = 2 sin3 t | x= sin t y = cos t + 2 sin 2t | ||
| x= cos3 t y = sin (t +1) sin t | x= sin t sin 2t y = cos t - 2 sin 2t | ||
| x= 2sin t y = cos t | x= cos 2t + sin t y = cos t - 2 sin 2t | ||
| x= cos3 t y = sin (t +1) | x= sin (t+1) y = cos t + 2 sin 2t | ||
| x= 0, 5sin t - cos 2t y = cos t – sin t | x= sin (t+1) y = cos (t +1) + 2 sin 2t | ||
| x= sin (t-1) y = cos (t +1) + 2 sin t | x= sin (t-1) y = cos (t +1) + 2 sin 2t | ||
| x= sin (t-1) y = cos (t -1) + 2 sin t | x= sin (t-1) y = cos (t -1) + 2 sin 2t | ||
| x= sin t - cos 2t y = cos t + 2 sin 2t | x= sin t - cos 2t y = cos t - 2 sin 2t |
Контрольные вопросы
1. Как построить декартовый график?
2. Как построить несколько графиков в одной системе координат?
3. Как изменить масштаб графика?
4. Как определить координату точки на графике?
5. Как построить гистограмму?
6. Какие средства имеются для форматирования графика?