Решение трансцендентного уравнения

Трансцендентные уравнения, как правило, не имеют аналитического решения. Они решаются численными методами с заданной погрешностью, которая определяется системной переменной TOL. Для решения одного уравнения с одним неизвестным используется функция root(f(x), x). Аргументами этой функции являются выражение и переменная, входящая в выражение. Функция возвращает значение переменной, которое обращает выражение в ноль.

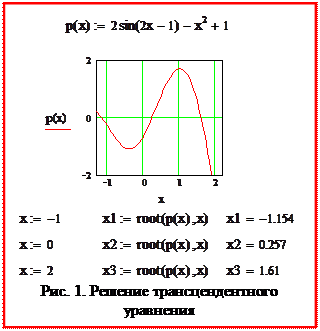Решение выполняется в следующей последовательности. Вначале определяется выражение, которое должно быть обращено в ноль. На рис. 13 это функция p(x). Затем строится график функции для определения числа корней уравнения. В примере (рис. 13) из графика следует, что задача сводится к отысканию трех корней.

Перед использованием функции root переменной x присваивается числовое значение − начальное значение. Присвоенное переменной x начальное значение становится первым приближением к искомому корню. Далее подключается функция root для определения значения первого корня, записываемого в переменную x1.

Когда значение выражения f (x) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным, и функция root возвращает результат. Результат можно увидеть, напечатав x1=.

Предлагаемая схема повторяется для остальных корней x2, x3 (рис. 13).

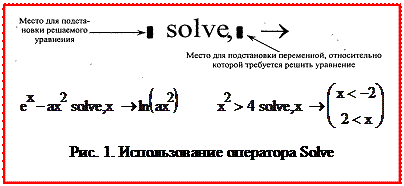Решение уравнения в символьном виде можно получить с помощью оператора Solve. При его вызове появляется шаблон с двумя маркерами для ввода (рис. 14). Решение выдается после выхода из зоны оператора автоматически.

Оператор Solve используется также для решения неравенств. Порядок применения тот же, что и при решении уравнений.