
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оценки эффективности инвестиций
|
|
Данные для оценки эффективности и выбора оптимального проекта представляются в виде таблицы.
Таблица 10.4. – Исходные данные
| № проекта | I | P1 | P2 | P3 | P4 |
| -400000 | |||||
| -420000 | |||||
| -400000 | |||||
| -420000 |
PV вычисляем по функции НПЗ (ЧПС) в меню «Вставка» «Функции» «Финансовые».
Функция НПЗ вычисляет чистый текущий объем вклада, используя учетную ставку, а также объемы будущих платежей (отрицательные значения) и поступлений (положительные значения).
Синтаксис
НПЗ(ставка; значение1; значение2;...)
Ставка - это учетная ставка за один период.
Значение1, значение2,... - это от 1 до 29 аргументов, представляющих расходы и доходы.
· Значение1, значение2,... должны быть равномерно распределены во времени, выплаты должны осуществляться в конце каждого периода.
· НПЗ использует порядок аргументов значение1, значение2,... для определения порядка поступлений и платежей. Убедитесь в том, что Ваши платежи и поступления введены в правильном порядке.
· Аргументы, которые являются числами, пустыми ячейками, логическими значениями или текстовыми представлениями чисел учитываются; аргументы, которые являются значениями ошибки или текстами, которые не могут быть преобразованы в числа, игнорируются.
· Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, тексты или значения ошибок в массиве или ссылке игнорируются.
· НПЗ аналогична функции ПЗ (текущее значение). Основное различие между функциями ПЗ и НПЗ заключается в том, что ПЗ допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода. В отличие от денежных взносов переменной величины в функции НПЗ, денежные взносы в функции ПЗ должны быть постоянны на весь период инвестиции.
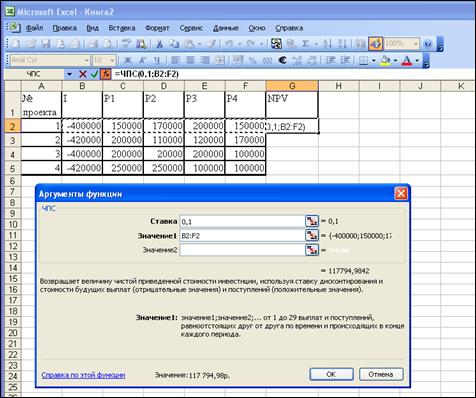
Рис. 10.1 – Определение чистого дисконтированного дохода по проектам
IRR вычисляем по функции “Финансовые” “ВНДОХ” (ВСД).
Возвращает внутреннюю скорость оборота для ряда последовательных операций с наличными, представленными числовыми значениями. Объемы операций не обязаны быть одинаковыми, как в случае ренты. Однако они должны происходить через равные промежутки времени, например, ежемесячно или ежегодно. Внутренняя скорость оборота - это процентная ставка дохода, полученного от инвестиции, состоящий из выплат (отрицательные значения) и поступлений (положительные значения), которые происходят в регулярные периоды времени.
Синтаксис:
ВНДОХ(значения; прогноз)
Значения - это массив или ссылка на ячейки, содержащие числовые величины, для которых вычисляется внутренняя скорость оборота средств.(ячейки прибыли и затрат)
· Значения должны включать по крайней мере одно положительное значение и одно отрицательное значение, для того, чтобы можно было вычислить внутреннюю скорость оборота.
· ВНДОХ использует порядок значений для интерпретации порядка денежных выплат или поступлений. Убедитесь, что Вы ввели значения выплат и поступлений в правильном порядке.
· Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются.
Прогноз - это величина, о которой предполагается, что она близка к результату ВНДОХ.
· Microsoft Excel использует метод итераций для вычисления ВНДОХ. Начиная со значения прогноз, функция ВНДОХ выполняет циклические вычисления, пока не получит результат с точностью 0, 00001 процента. Если функция ВНДОХ не может получить результат после 20 попыток, то возвращается значение ошибки #ЧИСЛО!.
· В большинстве случаев нет необходимости задавать прогноз для вычислений с помощью функции ВНДОХ. Если прогноз опущен, то он полагается равным 0, 1 (10 процентов).
· Если ВНДОХ выдает значение ошибки #ЧИСЛО!, или если результат далек от ожидаемого, можно попытаться выполнить вычисления еще раз с другим значением аргумента прогноз.
Пример расчета представлен в таблице.
Таблица 10.5 - Результаты расчета определения эффективности инвестиционных проектов
| № проекта | I | P1 | P2 | P3 | P4 | r | PV | NPV | PI | IRR | effekt |
| -400000 | 0, 10 | 529574, 48 | 129574, 48 | 1, 32 | 0, 24 | 0, 14 | |||||
| -420000 | 0, 10 | 478997, 34 | 58997, 34 | 1, 14 | 0, 17 | 0, 07 | |||||
| -400000 | 0, 10 | 416911, 41 | 16911, 41 | 1, 04 | 0, 12 | 0, 02 | |||||
| -420000 | 0, 10 | 577317, 12 | 157317, 12 | 1, 37 | 0, 30 | 0, 20 |
Оптимальное планирование портфеля инвестиций
Оптимальное планирование портфеля инвестиций можно выполнить с применением методов линейного программирования. Для этого необходимо сформировать экономико-математическую модель.
Целевая функция: чистая текущая стоимость проектов, включаемых в инвестиционный портфель, должна быть максимальной.
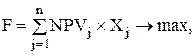 (10.6)
(10.6)
где Xj - целочисленная переменная, принимающая 2 значения:
- 0, если j проект не включается в план инвестиций;
- 1, если j проект включается в план инвестиций.
Ограничения на целевую функцию:
1. Каждая переменная Xj может принимать только дискретные знчения (0 или 1), что предполагает или полное финансирование проекта, или отказ от его включения в план.
Xj = 0, 1. (10.7)
2. Стоимость инвестиционного портфеля не должна превышать величины выделенных средств.
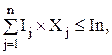 (10.8)
(10.8)
где Ij - величина инвестиций по j проекту;
In - наличие средств на инвестиционные цели.
Сформулированная задача может быть решена с применением методов целочисленного программирования.
Вопросы для самопроверки:
1. Каким образом применяются методы экономико-математического моделирования для оценки эффективности инвестиций?
2. Приведите примеры показателей оценки эффективности проекта.