
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Транспортная задача
|
|
Транспортная задача - задача определения оптимального плана перевозок груза из данных пунктов отправления в заданные пункты потребления.
Методы нахождение опорного решения транспортной задачи. Исходные данные транспортной задачи задаются в распределительной таблице, где по строкам отражают запасы груза у каждого поставщика, а по столбцам - потребность в данном грузе каждого потребителя. В правом верхнем углу каждой клетки - стоимость перевозки единицы груза от каждого поставщика каждому потребителю.
Сij – стоимость перевозки единицы груза, аi – запас груза у i – го поставщика (i =1…m), bi- потребность в грузе j- потребителя (j=1…n), х – кол-во груза от i-го поставщика к j –потребителю.
Постановка задачи (на мин-ую стоимость перевозки груза): найти значение переменных xij обеспечивающих целевой функции 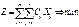 и удовлетворяющих системе ограничений: 1. Сумма всех грузов перевезенных от i-поставщика д.б. равна запасу груза у этого поставщика. 2. Сумма всех грузов, доставляемых j- потребителю д.б. равна потребности этого потребителя. 3. Неотрицательность переменных. Т.е.:
и удовлетворяющих системе ограничений: 1. Сумма всех грузов перевезенных от i-поставщика д.б. равна запасу груза у этого поставщика. 2. Сумма всех грузов, доставляемых j- потребителю д.б. равна потребности этого потребителя. 3. Неотрицательность переменных. Т.е.:
1 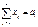 i=1…m
i=1…m
2  j=1…n
j=1…n
3 xij  0 i=1…m, j=1…n
0 i=1…m, j=1…n
Причем, для того чтобы решить транспортную задачу, сумма запасов однородного груза у поставщиков должна быть равна сумме потребностей в этом грузе потребителей (закрытая модель). 
В случае невыполнения этого условия (открытая модель) необходимо произвести некоторые преобразования (введениефиктивного поставщика илипотребителя) и получить закрытую модель.
Алгоритм решения транспортной задачи состоит из двух шагов:
- составление первоначального опорного плана каким-либо методом (минимального элемента в таблице, северо-западного угла, аппроксимации);
- улучшениеэтого плана и доведение его до оптимального методом потенциалов.
Рассмотрим алгоритм составления первоначального опорного плана методом аппроксимации. Данный метод особенно эффективен для задач малой размерностью, так как в большинстве случаев приводит к оптимальному решению.
В распределительной таблице добавляются нулевой столбец (слева) и нулевая строка (сверху).
В нулевую строку записываются разности, полученные в соответствующих столбцах путем вычитания наименьшей стоимости из следующей за ней по величине. В нулевой столбец заносят разности, полученные аналогично в строках. Из всех полученных разностей выбирается наибольшая. При этом могут встретиться два случая:
1. Одна наибольшая разность. Тогда в соответствующей строке (столбце) обычным образом заполняется клетка, в которой стоит наименьшая стоимость, и рассчитываются новые разности.
2. Несколько одинаковых наибольших разностей. В этом случае в соответствующей строке (столбце) находим клетку, в которой стоит наименьшая стоимость, и проверяем, будет ли этот показатель наименьшим в противоположном ряду.
Для строки противоположным рядом будем считать столбец, а для столбца - строку.
Здесь возможны следующие моменты:
- условие выполнено для одной клетки. Тогда с нее начинаем заполнение таблицы;
- условие выполнено для нескольких клеток. Тогда заполняется та, которой в противоположном ряду соответствует большая разность. Если противоположные разности равны, то заполняем обе клетки;
- условие не выполняется ни для одной клетки. Тогдав строках (столбцах) с наибольшей разностьюотыскивают наименьшую стоимость, из которой вычитают наименьшую стоимость противоположного ряда. В результате получают несколько положительных чисел. Заполняется клетка для которой это число будет наименьшим, после чего разности рассчитывают заново. Если числа будут одинаковыми, то заполняют любую клетку.
Условия оптимальности ТЗ (м/д потенциалов)
Для того чтобы проверить является ли данный опорный план оптимальным, необходимо применить метод потенциалов. Предварительно сделаем необходимые обозначения:
Vj - потенциалы столбцов;
Ui - потенциалы строк;
Cij - стоимость перевозки единицы груза от каждого поставщика каждому потребителю;
Хij - количество груза, которое будет перевезено от i-ro поставщика к j-му потребителю, где i =l,..., m(m-число строк), a j = 1,..., n (n - число столбцов).
Опорный план транспортной задачи может иметь (m + n -1) отличных от нуля неизвестных. В этом случае план является невырожденным.
Если отличных от нуля неизвестных меньше, чем (m+ n -1), то такой план - вырожденный. И для нахождения оптимального плана одна из пустых клеток таблицы, в этом случае, считается заполненной нулевым грузом.
Опорный план является оптимальным, если выполняются следующие условия:
1. Для заполненных клеток (Xij > 0)
Vi - Ui = Cij
2/ Для пустых клеток (Xij= 0)
Vi - Ui  Cij
Cij
для всех i= 1,..., m и j= 1,..., n.
Для всех пустых клеток, где нарушено второе условие оптимальности, находим характеристику по следующей формуле:  Vj-Ui-Cij
Vj-Ui-Cij
Из характеристик выбираем наибольшую и, начиная с клетки с данной характеристикой, строим цепь (цикл) — ломаная линия, вершины которой расположены в занятых клетках таблицы, кроме первой. Повороты цепи! делают под прямым углом. В строке или столбце, где проходит цепь, содержится только две клетки цепи, цепь должна быть замкнута. Клетки цепи отмечаем чередующимися знаками (+) и (-), начиная со знака (+) в первой клетке цепи. Из всех объемов поставок, стоящих в клетках со знаком (-), выбираем минимальный, он обозначается буквой Q. Вычитаем Q из поставок отрицательной полу цепи и прибавляем к поставкам положительной полу цепи.
Пересчитанные грузы записываем в таблицу и пересчитываем потенциалы.
Анализ планово-экономических задач с помощью к-та и оценок симплексных таблиц
Коэф-ты при свободных переменных в 1-вой симпл табл-це наз-ся технико-экономическими коэф-ми и показ-ют какие изменения произойдут в базисе при введении в него ед-цы размерности этой своб переменной. Сущ опред-ные правила введения в базис единицы размерности соотв переменной.
Правило 1. Если в базис вводится ед-ца размерности основной свобод переменной, то чтобы н-ти нов знач-я базис перем-х нужно из своб членов вычесть соотв коэф-ты столбца этой переменной с учетом знака.
Правило 2. Если в базис вводится ед-ца размерности дополнит свободной переменной, то чтобы н-ти нов знач-я бази-х переем-х нужно к своб членам прибавить соотв-щие к-ты столбца этой переменной с учетом знака.
К-ты бывшей разреш строки наз-ся к-тами взаимозаменяемости с (.) зрения диф-та ресурса.
Св-ва ДО: 1-ое связано с мерой дефицитности рес-сов. Если огр-е выпол-ся как строгое рав-во, то оц-ка б. ненулевая, если как нерав-во – то нулевая. Чем дефицитней рес-с, тем выше оц-ка. Исполь-е данного св-ва ДО позволяет вскрыть узкие места сдерж-щие рост произ-ва. Помогает выбрать правильное реш-е, если предполаг-ся расш-е произ-ва и треб-ся привл-е допол-х рес-в.
2. устойчивость оц-ки опт-ого пл. ДО уст-вы к изм-ю объемов произ-ых рес-ов, т.е. они не меняют своей вел-ны при изм-ии объемов произ-ых рес-ов довольно широких диапозонах изм-я, но они очень чувствительны к изм-ям вел-н коэф. цел. функ. и технико-экон. коэф.
3. связано с мерой влияния огран-я на функционал. ДО имеют ту же ед-цу измерения что и функционал. Ненул. оц показ-т как изм-ся вел-на функционала при введении в план ед-цы размерности св.п. По рес-сам (допол. перем): при увел. на ед-цу размерности функционал увел. на вел-ну оц. По продуктам (осн. перем): при увел. на ед-цу размерности данного продукта функционал умень на вел-ну оц-ки. Нулев. оц по рес-сам (продуктам) свид-т о том, что изм-я объема огран-я на ед-цу не повлияет на знач. функционала, т.к. рес-с по опт-му плану в избытке или продукт произведен сверх плана.
4.ДО- мера взаимозаменяемости рес-ов (продуктов), но не абсолютной, а относительной с точки зрения цел.функции
5. ДО- мера рент-ти отдель. спос-ов произ-ва. Те сп-бы, кот. вошли в опт-й пл рент-ны и суммарная оц. произ-ых рес-ов, затраченных по этому сп-бу будет равна той прибыли, кот. от него можно получить. Огр-я ДЗ будут выражены как строгие рав-ва. Для не рент-ых сп-ов суммарная оц-ка произ-ых рес-ов будет больше той прибыли, кот. дает этот СП-б, т.е. соот-щие огр-я ДЗ будет вып-но как строгое нер-во типа >.
Корректировка оптимального плана
Правило 1. Если в базис вводится основная переменная, то наибольшее значение которое она может принять определяется наименьшим отношением свободных членов к +-м коэффициентам столбца этой переменной. Правило 2. Если в план вводится дополнительная переменная, то наибольшее значение которое она может принять определяется наименьшим отношением свободных членов к отрицательным коэффициентам столбца этой переменной, взятых по абсолютной величине.
Экон. интепретация ДЗ. ДО опт-ого плана.
Левая часть ограничений ДЗ определяет суммарную денеж оц-ку всех производст ресурсов, затрач-х на 1 га посевов сотв культуры. Эта суммарн оц-ка дб не < той ст-ти валов прод-ции, кот-ю получ-т с 1 га соотв культуры. Целевой функц-ей ДЗ служит суммар оц-ка всех производст ресур-в, выдел на воздес всех культур. И эта оц-ка дб мин-ной.
Из теор двойст-ти следует, что Zmax=Wmin, те миним оц-ка всех производ ресур дб = той ст-ти валов прод-ции, кот м/получ при воздел этих культур.
Прямые зад.- зад., кот. обесп-т расчет опт-ого пл, а ДЗ – опт-х оц-к произ-ых рес-ов, кот. еще наз-т ДО.
Св-ва ДО: 1-ое связано с мерой дефицитности рес-сов. Если огр-е выпол-ся как строгое рав-во, то оц-ка б. ненулевая, если как нерав-во – то нулевая. Чем дефицитней рес-с, тем выше оц-ка. Исполь-е данного св-ва ДО позволяет вскрыть узкие места сдерж-щие рост произ-ва. Помогает выбрать правильное реш-е, если предполаг-ся расш-е произ-ва и треб-ся привл-е допол-х рес-в.
2. устойчивость оц-ки опт-ого пл. ДО уст-вы к изм-ю объемов произ-ых рес-ов, т.е. они не меняют своей вел-ны при изм-ии объемов произ-ых рес-ов довольно широких диапозонах изм-я, но они очень чувствительны к изм-ям вел-н коэф. цел. функ. и технико-экон. коэф.
3. связано с мерой влияния огран-я на функционал. ДО имеют ту же ед-цу измерения что и функционал. Ненул. оц показ-т как изм-ся вел-на функционала при введении в план ед-цы размерности св.п. По рес-сам (допол. перем): при увел. на ед-цу размерности функционал увел. на вел-ну оц. По продуктам (осн. перем): при увел. на ед-цу размерности данного продукта функционал умень на вел-ну оц-ки. Нулев. оц по рес-сам (продуктам) свид-т о том, что изм-я объема огран-я на ед-цу не повлияет на знач. функционала, т.к. рес-с по опт-му плану в избытке или продукт произведен сверх плана.
4.ДО- мера взаимозаменяемости рес-ов (продуктов), но не абсолютной, а относительной с точки зрения цел.функции
5. ДО- мера рент-ти отдель. спос-ов произ-ва. Те сп-бы, кот. вошли в опт-й пл рент-ны и суммарная оц. произ-ых рес-ов, затраченных по этому сп-бу будет равна той прибыли, кот. от него можно получить. Огр-я ДЗ будут выражены как строгие рав-ва. Для не рент-ых сп-ов суммарная оц-ка произ-ых рес-ов будет больше той прибыли, кот. дает этот СП-б, т.е. соот-щие огр-я ДЗ будет вып-но как строгое нер-во типа >.
17. Базовая структурная ЭММ задач, решаемых симплекснам м/дом
Базовая структурная ЭММ задач, решаемых симплекс-методом, имеет вид:
Целевая функция достигает экстремума
n
Z max (min)=S CjXj,
j=1
при условии выполнения трех ограничений:
1) по использованию производственных ресурсов - затраты i -ого ресурса на производство j - ой продукции не будут превышать наличного объема этого ресурса;
n
S aijxj£ bi iÎ I1
j=1
где
Xj - основная переменная, aij- норма затрат производственного ресурса i - го вида на единицу размерности j – ой, bi - объем ресурса
2) по заданному объему выполнения работ или производства продукции - объем производства продукции i -ого вида в расчете на единицу j-ой переменной будет не меньше гарантированного объема;
n
S vijxj ³ Qi iÎ I2 ,
j=1
где
vij - выход продукции i -го вида с единицы размерности j- ой переменной (урожайность, продуктивность).
Qi - гарантированный объем производства i -ого вида продукции.
3) условие неотрицательности переменных - поскольку искомые величины являются реальными положительными величинами (посевная площадь, поголовье, объем кормов и т.д.)
Xj ³ 0 j=1,..., n,
18. Базовая структурная ЭММ задач, решаемых распределительным м/дом
аi – кол-во груза у i пост-ка, bj – потреб-сть в этом грузе j потребителя, Сij – ст-ть (с/с) перевозки ед-цы груза от i пост-ка к j потреб-лю, Xij – кол-во груза, перевозимое от i пост-ка к j потр-лю.
Найти значение переменных Хij, где i=1-m, j=1-n, обеспеч-щих целевой ф-ции Z= m n
S ∑ Cij*Xij→ миним и удовлетвор след
i=1j=1
сис-ме ограничений: 1) Сумма всех грузов, перевозимых от i пост-ка дб = запасу груза у этого пост-ка
n
S xjj= ai, i=1-m.
j=1
2) Сумма всех грузов, доствляемых j потребителю д/равняться потребности этого потребителя:
m
S xjj= bj, j=1-n.
i=1
3) Условие неотриц-ти переменных: Хij> =0, j=1-n, i=1-m.
Если
m n
Sai=∑ bj, модель закрыта. Если не=, то
i=1 j=1 модель я/я открытой.
Чтобы сдела модель закрытой, необх ввести фиктивного пост-ка, если потребность > запаса или фиктивного потребителя, если запас > потребности. Целевая ф-ция обыч берется на минимум ст-ти перевозки груза или мин времени, затрач на перевозку груза.