
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача о смесях
|
|
Постановка задачи: составить наиболее экономичный рецепт смеси, сбалансированный по питательным элементам в расчёте на определённый вес (т, 100 гр, 1 кг, 100 кг), при этом содержание отдельных групп и видов компонентов смеси д.б. задано в определённых границах или в определённом соотношении.
Структурная эк.-математическая модель задачи: найти значение переменных xj, обеспечивающих в целевой функции
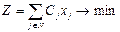 , и удовлетворяет следующей системе ограничений:
, и удовлетворяет следующей системе ограничений:
1. суммарный вес основных компонентов д.б. равен рассчитанному весу смеси 
2. по питат-му составу смеси. Колич. пит. веществ в расчетной весовой ед. смеси д.б. не менее заданной величины (в натур. выражении или в % к объёму смеси)
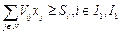 - множество, содержащее номера ограничений по содержанию пит. веществ в расчётной величине смеси.
- множество, содержащее номера ограничений по содержанию пит. веществ в расчётной величине смеси.
3. по соотношению отдельных переменных и их групп:
xj≥ (≤, =)Wijxij; xj≥ (≤, =) Wij∑ xj
∑ xj≥ Wij∑ xj,
где i принадлежит I 2, I 2 - множество, содержащее номера ограничений по содержанию отдельных компонентов и их групп
4. по границам отдельных видов компонентов и их групп (по структуре смеси)
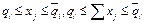
где i принадлежит I 3, I 3 - множество, содержащее номера ограничений по границам отдельных видов компонентов и их групп
5. неотрицательность переменных
xj≥ 0