Дисперсионный анализ

1. Применяют для того, чтобы установить оказывает ли существенное влияние на результат некоторый качественный фактор А, который имеет р уровней.

2. Используют также для того, чтобы установить значимо или не значимо различаются выборочные средние нескольких генеральных совокупностей (когда этих совокупностей достаточно много и их попарное сравнение затруднительно).

3. Иногда применяют, чтобы установить однородность нескольких совокупностей, однородные совокупности можно объединить в одну и получить о ней более полную информацию.

Дисперсионный анализ: однофакторный и многофакторный.

Постановка задачи: Пусть генеральные совокупности Х1, Х2, …Хр распределены нормально и имеют одинаковую, хотя и не известную дисперсию; математические ожидания также не известны, но могут быть различны. Требуется при заданном уровне значимости по выборочным средним проверить нулевую гипотезу о равенстве всех математических ожиданий: Н0: M[X1]= M[X2]=…= M[Xp]

Основная идея – сравнение «факторной дисперсии», порождаемой воздействием фактора и «остаточной дисперсии», обусловленной случайными причинами. Если различие между этими дисперсиями значимо, то фактор оказывает существенное влияние на Х, в этом случае средние наблюдаемых значений на каждом уровне (групповые средние) различаются так же значимо.

Схема однофакторного дисперсионного анализа:

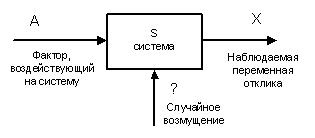Фактор А изменяется на р уровнях

Основная гипотеза, проверяемая дисперсионным анализом: Уровни фактора А не влияют на математическое ожидание величины Х.

Основная идея дисперсионного анализа: Поскольку на Х кроме фактора А воздействуют и случайные причины, наблюдения одной и той же группы рассеяны вокруг своей групповой средней, следовательно, для оценки влияния случайных причин целесообразно составить сумму квадратов отклонений наблюдаемых значений каждой группы от своей групповой средней. 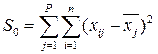S₀ – Характеризует воздействие случайных причин

S[X]=S_A[X]+S₀[X]

Основные предположения, необходимые для применения дисперсионного анализа:

1. Случайная величина Х распределена по нормальному закону

2. Все частные дисперсии однородны, то есть их различия не различимы.

Последовательность дисперсионного анализа:

1. Заполнение дисперсионной таблицы, расчет средних значений и дисперсий

2. Проверка данных на соблюдение условий применения инструментария дисперсионного анализа: данных в каждой строке таблицы на нормальность распределения и проверка однородности дисперсий при разных уровнях фактора

3. Расчет оценок дисперсии случайной величины

4. Проверка гипотезы о равенстве дисперсий по критерию Фишера

5. Если гипотеза о равенстве дисперсий отклоняется, то по критерию Стьюдента выполняется сравнение средних для разных уровней фактора