Модели турбулентности, основанные на гипотезе Буссинеска

Первая часть моделей, основанная на гипотезе Буссинеска

Устанавливает связь между корреляциями и средним течением. Эта связь устанавливается посредством коэффициента турбулентной (кажущейся) вязкости. Эта связь получена из аналогии с молекулярной вязкостью. Однако, предположения, справедливые для молекулярного движения, не обязательно будут справедливы для макроскопического.

Неизвестна здесь турбулентная вязкость m_t. Турбулентная вязкость не является физическим свойством среды. Турбулентная вязкость – свойство потока.

Основываясь на анализе размерностей, m_t может быть определена по двум масштабам: длины и времени (или скорости)

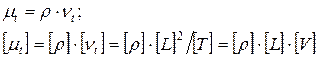
Наиболее простыми моделями турбулентности являются алгебраические модели Прандтля, Кармана и др.

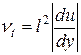
Более сложными являются модели, которые используют дифференциальное уравнение (одно или несколько) для нахождения m_t.

В зависимости от числа уравнений, и соответственно, неизвестных параметров, выделяют однопараметрические, двухпараметрические и др. модели.

Из анализа размерностей кинетическая энергия турбулентности:

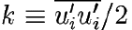
[L²/T²]

Скорость диссипации кинетической энергии турбулентности

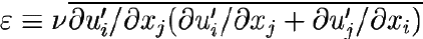
[L²/T³]

Удельная скорость диссипации кинетической энергии турбулентности

w= e/k

[1/T]

Однопараметрическая модель Спалларта-Аллмареса:

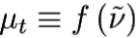
Двухпараметрические стандартная, RNG и realizable модели

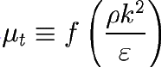
Двухпараметрические стандартная k-w и SST k-w