Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кардиналистский подход
|
|
Кардиналисты (экономисты 19 века – У. Джевонс, К. Менгер, Л. Вальрас) в основе их теории лежало предположение о возможности соизмерения полезности различных благ. Согласно этой теории ценность (стоимость) блага определяется не затратами труда, а потребностью, которая удовлетворяется данным благом, и субъективная полезность блага зависит от степени редкости блага и от степени насыщения потребности в нём.
Кардиналисты считали, что потребитель в состоянии оценивать потребляемые им товары с точки зрения величины полезности, приносимой ими. Причем целью потребителя является максимизация полезности. При этом полезность от потребления товара зависит лишь от количества потребляемых единиц этого товара.
Например, потребитель может сказать, что ежедневное потреблениеим 1 яблока приносит ему удовлетворение, скажем 20 ютилов, ежедневное потребление 2 яблок – 38 ютилов, ежедневное потребление 2 яблок и 1 сигареты и 1 апельсина – 63 ютила и т.д.
Причем количественная оценка полезности того или иного товара или товарного набора имеют исключительно индивидуальный субъективный характер.
Данную теорию еще называют количественной, т.к. предполагается что потребитель может дать количественную оценку в ютилах полезности любого потребляемого им товарного набора.
Формально это можно записать в виде функции общей полезности:
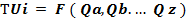(2.1),
где
TUi - общая полезность данного товарного набора;
Qa, Qb. … Q z – объемы потребления товаров А, В, Z в единицу времени.
Большое значение имеют предположения о характере функции общей полезности.
Зафиксируем объемы потребления товаров В, С,..., Z. Рассмотрим, как изменяется общая полезность товарного набора в зависимости от объема потребления товара А (например, яблок). В верхней части рис. 2.1, а изображена эта зависимость. Длина отрезка ОК равна полезности товарного набора при фиксированных нами объемах товаров В, С,..., Z при нулевом объеме потребления товара А. В количественной теории предполагается, что функция ТU в верхней части рис. 2.1 а возрастающая (чем больше яблок, тем большую полезность имеет товарный набор) и выпуклая вверх (каждое последующее яблоко увеличивает общую полезность товарного набора на меньшую величину, чем предыдущее). В принципе эта функция может иметь точку максимума (S), после которой она становится убывающей (представьте, что Вас ежемесячно заставляют потреблять по 100 кг яблок).
В нижней части рис. 2.1 а изображена зависимость предельной полезности яблок от объема их потребления.
Предельная полезность — это прирост общей полезности товарного набора при увеличении объема потребления данного товара на одну единицу.
Математически предельная полезность товара есть частная производная общей полезности товарного набора (2.1) по объему потребления i-того товара:
= 
.
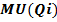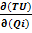Геометрически значение предельной полезности (длина отрезка ОN) равно тангенсу угла наклона касательной к кривой TUв точке L. Поскольку линия TU выпукла вверх, с увеличением объема потребления i-того товара угол наклона этой касательной уменьшается и, следовательно, понижается и предельная полезность товара. Если при некотором объеме его потребления (на нашем рисунке QA//) функция общей полезности достигается максимума, то одновременно предельная полезность товара становится нулевой [3, с. 105-106].
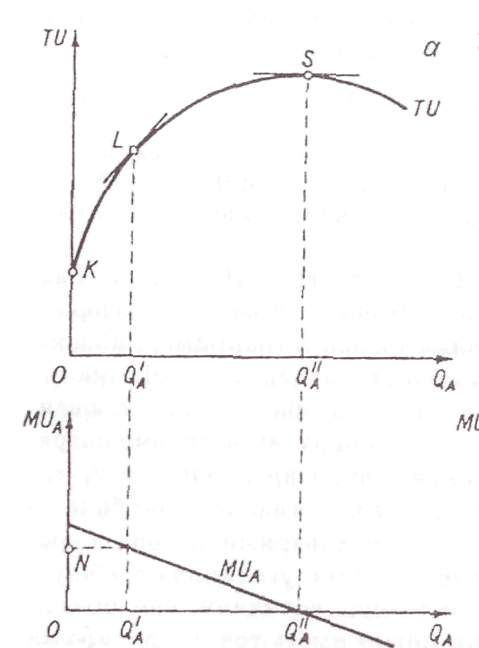
Рис. 2.1. Общая и предельная полезность.
Таким образом, в соответствии с количественной теорией функция полезности имеет две черты:
1- является возрастающей, т.к. каждая последующая единицы запаса повышает общею полезность блага
2- каждая последующая единица приносит меньшее повышение общей полезности, чем предыдущая, поскольку действует закон снижения предельной потребности потребителя.
Оптимальная функция полезности позволяет представить систему предпочтений потребителя в случае потребления одного единственного товара. В случае наличия набора товаров полезность представляется как сумма полезности товаров, входящих в набор. Данная функция представляется следующим образом:
(2.2),
где
U – общая полезность от всего набора потребляемых товаров
U1 – Un - полезность от потребления товаров (1-n)
1 – n – объем потребления товаров (1-n)
Правило кардиналистов заключается в таком распределении денежного дохода потребителя, при котором последняя денежная единица, затраченная на приобретение каждого вида продуктов, приложена на равную предельную полезность.
Т.е. правило максимизации полезности - потребитель максимизирует свою полезность, распределяя доход таким образом, что каждая последняя денежная единица, затраченная на приобретение любого блага, приносит одинаковую предельную полезность:
= 
= … 
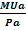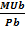= λ, (2.3)
где λ – некоторая величина, характеризующая предельную полезность денег (средняя предельная полезность по бюджету покупателя).
Иначе можно записать,
= 
, …. 
= 
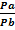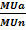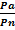(2.4)
В такой ситуации никто не будет побуждать потребителя к изменению структуры расходов, он будет находиться в состоянии равновесия. Более того, ему невыгодно изменять структуру потребления, поскольку такое изменение только ухудшит его благосостояние.
Т.о. в оптимуме (максимум полезности при данных вкусах потребителя. ценах и доходах) полезность, извлекаемая из последней денежной единицы, потраченной на покупку какого-либо товара, одинакова, независимо, от того на какой именно товар она израсходована. (2 закон Госсена).
Т.к. предельная полезность экономического блага для потребителя снижается, то производитель может продать дополнительное количество своей продукции лишь в том случае, если снизит цену [4. c. 24-25].