К работе с цифрами и процентами

Исследователь оперирует различным цифровым материалом: показаниями в опытах и наблюдениях, средними величинами, процентами и др. Хотя студент с цифрами работает постоянно, нередко он допускает досадные ошибки. Так, при вычислении средних значений не всегда обращают внимание на их точность. Например, диаметр стволов измерялся с точностью ± 1 см, а при вычислении среднего диаметра его приводят к точности до 0, 001 см (до 0, 01 мм). На сделанное замечание ответ типа: «Так машина посчитала» не добавляет симпатий к такому студенту. Обычно среднее значение выводится с точностью на один порядок выше, чем был исходный материал. Например, диаметр стволов измерялся с точностью ± 1 см, следовательно, средний диаметр записывается до 0, 1 см, а высота, если она измерялась с точностью ± 1 дм, то средняя должна быть вычислена и записана до 0, 1 дм (1 см).

Количество значащих, т.е. верных, цифр соответствует той части числа, которая считается точной. Так, если измерение составило 17, 6 г, то считается, что оно точно до 0, 1 г, т.е. истинное его значение между 17, 55 и 17, 65 г. Точно так же истинное значение 17, 5 находится между 17, 46 и 17, 54.

Произведение или частное, полученное из округления чисел, не должно записываться с бó льшим количеством значащих цифр, чем их имеется у каждого из чисел, с которыми производятся действия. Если же у чисел разное количество десятичных знаков, то ориентироваться следует на наименьшее количество. Примеры: 3, 1 2, 7 = 8, 4 (правильно), а не 8, 37 (неверно), 3, 102, 70 = 8, 37 (правильно); 6, 27: 13 = = 0, 48 (а не 0, 482).

При округлении цифр следуют правилу Гаусса: если после цифры 5 следует цифра, отличная от нуля, то к предшествующему десятичному знаку прибавляется единица; если же после 5 идут нули и если последующие знаки неизвестны, то в случае четного предшествующего знака отбрасывается 5, а в случае нечетного прибавляется единица. Так, число 1, 75 при округлении до 0, 1 записывается 1, 8, а 2, 65 округляется в 2, 6. Правильное округление числа 1, 34456 будет: 1, 3446, 1, 345, 1, 34 (а не 1, 35), 1, 3 и 1.

При анализе научного материала часто вычисляют проценты. Их подразделяют на простые и сложные. В лесном хозяйстве чаще всего рассчитывают простые проценты. Например, диаметр ствола в 40 лет составил 20 см, а в 55 – 24 см. Увеличение диаметра составило 4 см, или (4·100/20) = 20%. При сравнении хода роста древостоев по высоте, диаметру двух и более типов леса простые проценты вычисляются часто. Например, в возрасте 100 лет средняя высота древостоя оказалась равной в типе леса С лп 27, 3 м, в С ртр – 25, 8 м, а в С яг – 24, 4 м. По сравнению с С лп высота в С ртр ниже на 1, 5 м (5, 5 %), а в С яг – на 2, 9 м (10, 6 %). Если сравнивать с высотой С ртр, то результаты будут следующие: в С лп высота больше на 1, 5 м (5, 8 %), а в С яг меньше на 1, 4 м (5, 4 %). При сравнении с типом леса С яг результаты также будут отличными: в С лп высота древостоя на 2, 9 м (11, 9 %) больше, а в С ртр – на 1, 4 м или на 5, 7 %.

Расчет сложных процентов обычно делают при вычислении средних темпов роста или прироста деревьев и древостоев. Например, если объем ствола за четыре года увеличилось на 43 %, то среднегодовой темп роста (или процент прироста) по объему р_v составил:

p_v = 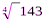= 3, 5 (%).

Заметим, что для извлечения корней при этом часто приходится прибегать к логарифмированию чисел.

При определении процентов прироста по высоте, диаметру, сумме площадей сечений и объему ствола используется формула Преслера:

P_T = ,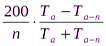

где P_T – процент прироста (по объему, диаметру или высоте ствола), %;

п – число лет, за которое определяется процент прироста;

Т_а – таксационный признак (объем, диаметр или высота ствола) теперь;

Т_а-п – таксационный признак (объем, диаметр или высота ствола) п лет назад.

Пример. Пусть объем ствола равен 0, 240 м³, а пять лет назад он был 0, 210 м³. Определим процент прироста по объему по формуле Преслера (1), простых (2) и сложных (3) процентов:

P_v == = 2, 7 (%), (1)

P_v = 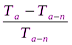· = · = 2, 9 (%), (2)

P_v = 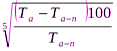= = 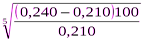= 2, 6 (%). (3)

Из примера видно различие процентов прироста по объему ствола, вычисленных по трем формулам. При этом величина показателя, полученная по формуле Преслера, занимает промежуточное положение: меньшее, чем по формуле простых процентов и большее, чем по формуле сложных.

Контрольные вопросы

1. Как подобрать объекты в лесу для научного исследования?
2. На что обратить внимание при изучении хода роста древостоев?
3. Особенности опытов с рубками ухода.
4. Особенности исследований с лесными культурами.
5. В чем заключается проверка и отбраковка сомнительных данных?
6. Как правильно составить вариационный ряд?
7. Правила вычисления статистик при небольшом числе наблюдений.
8. Особенности вычисления статистик при большом числе наблюдений.
9. Сравнение вариационных рядов.
10. Как вычислить ошибку уравнения?
11. Корреляционный анализ.
12. Дисперсионный анализ.
13. Правильное округление цифр.
14. Вычисление простых и сложных процентов.