
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Регрессионный анализ и точность уравнения
|
|
Регрессией называют изменение функции при изменении аргументов. Задача регрессионного анализа состоит в выравнивании опытных данных, получении уравнений, наиболее точно описывающих реальную действительность, и оценке их точности.
Выравнивание опытных данных чаще всего выполняется по способу наименьших квадратов с подбором различных аналитических уравнений. В лесном хозяйстве большинство зависимостей передается уравнениями прямой линии, кривой второго и третьего порядка. Значительно реже используют логарифмическую, показательную и другие функции.
Выравнивание экспериментальных данных легко выполняется на компьютере по стандартным программам, например в Exсel. Программа позволяет быстро получить уравнение кривых различного порядка и по коэффициенту детерминации R (коэффициент корреляции в квадрате r2 или корреляционное отношение в квадрате  ) выбрать наиболее точно отражающее фактическую зависимость. Выбирается обычно из нескольких одно уравнение, величина коэффициента детерминации у которого наибольшая. При этом, если коэффициент детерминации равен от 0, 01 до 0, 10, теснота связи считается слабой, от 0, 11 до 0, 25 – умеренной, 0, 26-0, 50 – значительной, 0, 51-0, 80 – высокой и при 0, 81 и более – очень высокой. В практическом плане в большинстве случаев при выравнивании высот, диаметров стволов, сумм площадей сечений, запасов и других показателей у древостоев удается получить уравнения сR0, 90-0, 99, т.е. с очень высокой аппроксимацией эмпирических и теоретических данных.
) выбрать наиболее точно отражающее фактическую зависимость. Выбирается обычно из нескольких одно уравнение, величина коэффициента детерминации у которого наибольшая. При этом, если коэффициент детерминации равен от 0, 01 до 0, 10, теснота связи считается слабой, от 0, 11 до 0, 25 – умеренной, 0, 26-0, 50 – значительной, 0, 51-0, 80 – высокой и при 0, 81 и более – очень высокой. В практическом плане в большинстве случаев при выравнивании высот, диаметров стволов, сумм площадей сечений, запасов и других показателей у древостоев удается получить уравнения сR0, 90-0, 99, т.е. с очень высокой аппроксимацией эмпирических и теоретических данных.
Программа Exсel (в отличие от STATGRAPHICS), к сожалению, не вычисляет ошибку полученного уравнения. Поэтому ее приходится определять отдельно. Для этого составляется вспомогательная таблица (табл. 4.8), в которую вписываются исходные данные (1-я строка) и выравненные с помощью Exсel(2-я строка). В качестве примера использованы данные средних высот древостоев в возрасте от 10 до 79 лет.
Таблица 4.8
Опытные и выравненные данные средних высот в различном возрасте древостоев
| Показатели | Возраст, лет | |||||||||
| Ноп, м | 3, 4 | 5, 2 | 7, 2 | 8, 3 | 10, 0 | 12, 5 | 13, 0 | 15, 0 | 15, 9 | 17, 1 |
| Нвыр, м | 3, 5 | 5, 5 | 7, 0 | 8, 8 | 10, 0 | 12, 0 | 13.6 | 15, 0 | 16.1 | 16, 8 |
| Ноп- Нвыр | -0, 1 | -0, 3 | +0, 2 | -0, 5 | +0, 5 | -0.6 | -0, 2 | -0, 3 | ||
| (Ноп- Нвыр)2 | 0, 01 | 0, 09 | 0, 04 | 0, 25 | 0, 25 | 0, 36 | 0, 04 | 0, 09 |
Связь возраста А и средней высоты древостоев Н аппроксимируется кривой второго порядка:
Н = -0, 0017 А2 + 0, 3505 А + 0, 12; R = 0, 995.
Ошибка (точность) уравнения вычисляется по формуле
My = ±  ,
,
где 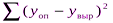 – сумма квадратов отклонений между опытными (фактическими) данными и вычисленными по уравнению (сумма значений последней строки табл. 4.8);
– сумма квадратов отклонений между опытными (фактическими) данными и вычисленными по уравнению (сумма значений последней строки табл. 4.8);
п – количество точек линии регрессии, по которым вычислено уравнение (в табл. 4.8 их 10: 1-я – 3, 4; 2-я – 5, 2 и т.д.);
е – количество коэффициентов уравнения (в примере для уравнения кривой второго порядка их 3).
My = ± = ±  = ±
= ± 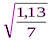 = ±
= ±  = ± 0, 40 (м).
= ± 0, 40 (м).
Следовательно, уравнение зависимости средней высоты древостоев Н от возраста А следует записать так:
Н = -0, 0017 А2 + 0, 3505 А + 0, 12 ± 0, 40 (м).