Исследование и сравнение вариационных рядов

При изменчивости случайной величины в зависимости от множества факторов возникает необходимость проверки выборки на подчинение закону нормального распределения. Она проводится, как известно, при помощи показателей асимметрии А и эксцесса Э и их ошибок.

Для вычисления А и Э необходимо вычислить центральные моменты µ₂ , µ₃иµ₄:

µ₂= m₂ – m₁² = 3, 05 – 0, 15²= 3, 03;

µ₃ = m₃ – 3 m₂ m₁ + 2 m₁³ = -0, 48 – 3·3, 05 ·(-0, 15) + 2·(-0, 15)³= 0, 88;

µ₄= m₄ – 4 m₃m₁ + 6 m₂m₁² – 3 m₁⁴ = 21, 28 – 4·(-0, 48)·(-0, 15) +

+6·3, 05 (-0, 15)² – 3(-0, 15)⁴= 21, 28 – 0, 29 + 0, 41 – 3, 00 = 18, 40.

Асимметрия (мера косости) равна:

А = 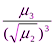= = 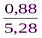0, 17.

(При А < 0, 5 косость считается малой, при величине от 0, 5 до 1 – средней и если А > 1 – большой.)

Эксцесс (мера крутости) равняется:

Э = 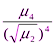-3 = 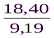-3 = -1, 00.

Основные ошибки А и Э вычислим, используя приближенные формулы:

m_A = 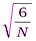= = 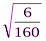0, 194; m_Э = 2= 2= 0, 388.

Достоверность косости t_A = A: m_A = 0, 17: 0, 194 = 0, 88 (< 4, следовательно, достоверность косости не подтверждается).

Достоверность крутости t_Э = Э: m_Э = -1, 00: 0, 388 = -2, 58 (< 4, следовательно, достоверность крутости также не подтверждается).

Таким образом, отклонение крутости кривой от нормальной не доказано, а с учетом достоверности косости можно сделать вывод, что кривая соответствует закону нормального распределения.

Для проверки выборки на соответствие ее закону нормального распределения лучше использовать квадратичные отклонения асимметрии _А и эксцесса _Е. Если хотя бы один из показателей А или Э по абсолютной величине превосходит в два и более раз соответствующее квадратичное отклонение, то нормальность распределения случайной величины является недоказанной.

Вычислим средние квадратичные отклонения А и Э (в формулах N – количество наблюдений в выборке):

_А = 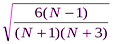= = 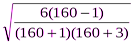0, 19;

_Е = 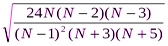= = 0, 15.

Отношение А к _А составило 0, 89, а Э к _А – 6, 7. Следовательно, проверка на нормальность распределения, вычисленная вторым способом, не подтвердилась.

Достаточно распространенной задачей при исследованиях в лесном хозяйстве является сравнение выборок и оценка их различий. При сравнении малых выборок (N ≤ 30) применяют тест серий, ранговый тест, критерий Колмогорова-Смирнова, критерий Стьюдента, тест знаков для зависимых выборок. Для больших выборок (N > 30) оценку производят через критерий Стьюдента, непараметрический тест Сиджела-Тьюки, параметрический метод Фишера (Терентьев, Ростова, 1977).

Тест серий (Вальда-Вольфовича) улавливает различия по положению, характеру распределения и по разбросу сравниваемых рядов распределения.

Ранговый тест Уилкоксона основан на анализе объединенного ранжированного ряда. Он учитывает как общее размещение вариант, так и размеры серий.

Критерий Колмогорова-Смирнова основан на предположении о непрерывном распределении изучаемого признака в генеральной и выборочной совокупности.

Критерий Стьюдента t применяется при малых и больших выборках. Его часто используют научные работники в своих исследованиях и поэтому целесообразно привести его формулу:

t = ,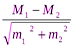

где М ₁, М ₂– средние значения соответственно первой и второй выборок;

m ₁, m ₂ – основные ошибки средних значений.

Вычисленное по формуле значение t далее сравнивается со стандартным значением по таблице Стьюдента с учетом числа степеней (берется равным сумме числа наблюдений двух выборок за исключением двух) для определенного уровня значимости р (0, 95; 0, 99 или 0, 999). Если фактическое значение меньше стандартного, то различие считается недостоверным.

При сравнении средних показателей двух больших выборок, если показатель t равен 3 и более, можно считать различие существенным (при вероятности р = 0, 999).

Тест знаков относится к простейшим методам оценки различий между зависимыми переменными. Значения сравниваемых рядов записываются в строчки, причем чтобы первое значение второго ряда было под таким же в первом и т.д. Затем в парах значений определяется направление – увеличение (+) или уменьшение (-) – и подсчитывается число пар с реже встречающимся направлением изменения. Полученные значения сравниваются затем с табличными данными.

Тест Сиджела-Трюки основан на ранговой оценке разброса вариант в ранжированном ряду. При этом первому значению присваивается ранг 1, второму – 2 и т.д. Затем вычисляется значение теста по формуле и сравнивается с табличным значением.

Критерий ФишераF, как и критерий Стьюдента, находит довольно частое применение. Он основан на оценке выборочных дисперсий σ ²:

F = ,

где σ ₁ и σ ₂ – средние квадратичные отклонения первой и второй выборок.

Если фактическое значение критерия Фишера будет больше стандартного (табличного), то различие считается доказанным.