
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Отбраковка сомнительных данных
|
|
Массовые наблюдения и эксперименты, полученные в лесу на пробных площадях, опытных делянках, лесных культурах или в лесном питомнике, представляют собой набор цифр. Чтобы статистически обработать цифровой материал, необходимо составить вариационный ряд (или ряды).
Довольно часто возникает ситуация, когда в ранжированном ряду оказываются числа, вызывающие сомнения (из-за ошибки наблюдателя, прибора, патологии данного растения или его части и т. п.). Их следует проверить на принадлежность к данной совокупности. Эта работа выполняется перед обработкой вариационных рядов. В случае значительного «отскока» они должны быть отбракованы, т. е. исключены из дальнейших расчетов. Для этого используют формулы для проверки сомнительных значений. Если сильно отклоняется одно минимальное значение в ряду, то применяется критерий  , вычисляемый по уравнению
, вычисляемый по уравнению
= (Х2 - Х1) / (Хn- Х1),
где Х1 – первое (сомнительное) значение в ранжированном ряду,
Х2 – второе,
Хn – последнее.
Полученное значение после этого сравнивают с табличным (табл. 4.1) при Р0, 95или Р0, 99.
Пример. Измерена длина побегов, см: 3, 7; 5, 2; 5, 4; 5, 4; 5, 5; 5, 5; 5, 8; 5, 9; 6, 0. В данном ряду измерений вызывает сомнение первое значение (3, 7). Вычисляем:
= (5, 2-3, 7) / (6, 0-3, 7) = 0, 652, что больше табличного значения (n= 9) 0, 437. Следовательно, первое значение должно быть отбраковано, т.е. не должно включаться в расчет.
Таблица 4.1
Критические значения и  для исключения крайних вариант (1 – одного значения, 2 – двух значений)
для исключения крайних вариант (1 – одного значения, 2 – двух значений)
| n | n | ||||||||
| Р0, 95 | Р0, 99 | Р0, 95 | Р0, 99 | Р0, 95 | Р0, 99 | Р0, 95 | Р0, 99 | ||
| 0, 941 | 0, 988 | 1, 000 | 1, 000 | 0, 412 | 0, 527 | 0, 531 | 0, 632 | ||
| 0, 765 | 0, 889 | 0, 967 | 0, 992 | 0, 392 | 0, 502 | 0, 504 | 0, 603 | ||
| 0, 642 | 0, 780 | 0, 845 | 0, 929 | 0, 376 | 0, 482 | 0, 481 | 0, 579 | ||
| 0, 560 | 0, 698 | 0, 736 | 0, 836 | 0, 338 | 0, 438 | 0, 430 | 0, 522 | ||
| 0, 507 | 0, 637 | 0, 661 | 0, 778 | 0, 300 | 0, 391 | 0, 372 | 0, 464 | ||
| 0, 468 | 0, 590 | 0, 607 | 0, 710 | 0, 281 | 0, 367 | 0, 347 | 0, 434 | ||
| 0, 437 | 0, 555 | 0, 565 | 0, 667 | 0, 260 | 0, 341 | 0, 322 | 0, 402 |
Для проверки одной максимальной варианты используется критерий:
= (Хn- Хn-1) / (Хn- Х1),
где Хn – последнее значение (варианта),
Хn-1 – предпоследнее значение (варианта).
Пример. Измерена длина листьев у дерева, см: 4, 9; 5, 2; 5, 4; 5, 4; 5, 5; 5, 5; 5, 8; 5, 9; 6, 0; 6, 5. В данном ряду измерений вызывает сомнение последнее значение (6, 5). Вычисляем:
= (6, 5–6, 0) / (6, 5–4, 9) = 0, 5: 1, 6 = 0, 312, что меньше 0, 412. Следовательно, последнее значение следует включить в расчеты, т.е. оно не должно отбраковываться.
Если сомнительными являются два крайних значения и при этом оба находятся в одном из концов ранжированного ряда, то их оценка производится по или  :
:
= (Х3 –Х1) / (Хn - Х1) (для Х1 и Х2);
или
= (Хn –Xn-2) / (Хn - Х1) (для Хn и Хn-1).
Пример. Измерена толщина коры у деревьев на высоте 1, 3 м, см: 0, 6; 0, 6; 0, 9; 1, 2; 1, 4; 1, 4; 1, 5; 1, 5; 1, 8; 1, 9; 2, 0; 2, 1. Вызывают сомнения первые два значения вариационного ряда. Вычисляем:
= (0, 9-0, 6) / (2, 1 - 0, 6) = 0, 3 / 1, 5 = 0, 200.
Полученный результат меньше табличного значения (0, 376), поэтому первые два значения ряда относятся к данной совокупности, а потому не требуют исключения в дальнейших расчетах.
Пример. Измерена толщина коры у деревьев на высоте 1, 3 м, см: 1, 2; 1, 4; 1, 4; 1, 5; 1, 5; 1, 8; 1, 9; 2, 0; 2, 1; 2, 8; 2, 9. В этом рядувызывают сомнение два последних значения. Также вычисляем:
= (2, 9 -2, 1) / (2, 9 -1, 2) = 0, 8 / 1, 7 = 0, 470.
Полученный результат больше табличного значения (0, 392), поэтому последние два значения ранжированного ряда не относятся к данной совокупности и потому должны быть исключены при его дальнейшей обработке.
При двух сомнительных значениях в ранжированном ряду, когда одновременно одно из них минимальное, а другое максимальное, для их проверки употребляют критерий или:
= (Х2 –Х1) / (Хn-1 - Х1) (для оценки Х1) или
= (Хn –Хn-1) / (Хn – Х2) (для оценки Хn).
Для оценки используется табл. 4.2.
Пример. Измерена высота подроста на участке одной породы и одного возраста, м: 0, 3; 0, 9; 1, 2; 1, 4; 1, 4; 1, 6; 1, 8; 1, 9; 1, 9; 2, 4; 3, 5. В данном ряду вызывают сомнение начальное и конечное значения. Вычисляеми:
= (0, 9 – 0, 3) / (2, 4 – 0, 3) = 0, 6 / 2, 1 = 0, 286;
= (3, 5 – 2, 4) / (3, 5 - 0, 9) = 1, 1 / 2, 6 = 0, 423.
Таблица 4.2
Критические значения идля исключения крайних вариант
| n | Р0, 95 | Р0, 99 | n | Р0, 95 | Р0, 99 | n | Р0, 95 | Р0, 99 |
| 0, 955 | 0, 991 | 0, 410 | 0, 520 | 0, 320 | 0, 414 | |||
| 0, 807 | 0, 916 | 0, 395 | 0, 502 | 0, 314 | 0, 407 | |||
| 0, 689 | 0, 805 | 0, 381 | 0, 486 | 0, 309 | 0, 400 | |||
| 0, 610 | 0, 740 | 0, 369 | 0, 472 | 0, 304 | 0, 394 | |||
| 0, 554 | 0, 683 | 0, 359 | 0, 460 | 0, 299 | 0, 389 | |||
| 0, 512 | 0, 635 | 0, 349 | 0, 449 | 0, 295 | 0, 383 | |||
| 0, 477 | 0, 597 | 0, 341 | 0, 439 | 0, 291 | 0, 378 | |||
| 0, 450 | 0, 566 | 0, 334 | 0, 430 | 0, 287 | 0, 374 | |||
| 0, 428 | 0, 541 | 0, 327 | 0, 421 | 0, 283 | 0, 369 |
Полученные результаты и для n = 11 оказались меньше табличных значений для Р0, 95и Р0, 99(0, 450 и 0, 566). Следовательно, оба крайних значения относятся к данной совокупности и не должны исключаться при дальнейшей обработке ряда.
Более надежным способом проверки принадлежности вариант к рассматриваемому рядуявляется вычисление 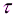 по формуле с использованиемосновного отклонения σ:
по формуле с использованиемосновного отклонения σ:
= I xi – М I: σ
где М – среднее арифметическое значение (вычисляется без отбрасывания сомнительных вариант);
σ – основное отклонение вариант;
xi – сомнительная варианта.
Полученное значение сравнивают с табличным при Р0, 95или Р0, 99(табл.4.3).
Для сравнения воспользуемся уже рассмотренным примером. Сопоставим результат проверки принадлежности сомнительной варианты к одному ряду на примере измерения длины побегов, приведенного выше.
М= 5, 4 см; σ = 0, 68 см; = I3, 7 – 5, 4 I/ 0, 68 = 2, 50.
При п = 9 Р0, 95= 2, 35, Р0, 99= 2, 53. Таким образом, значение 3, 7 см на уровне Р0, 95 следует исключить при дальнейшей обработке, а на уровне Р0, 99гипотеза принадлежности первой варианты к другой совокупности не подтверждается.
Таблица 4.3
Критические значения для исключения крайних вариант при Р0, 95и Р0, 99
| n | Р0, 95 | Р0, 99 | n | Р0, 95 | Р0, 99 | n | Р0, 95 | Р0, 99 |
| 2, 07 | 2, 16 | 2, 80 | 3, 11 | 3, 28 | 3, 64 | |||
| 2, 18 | 2, 31 | 2, 82 | 3, 13 | 3, 33 | 3, 70 | |||
| 2, 27 | 2, 43 | 2, 84 | 3, 16 | 3, 37 | 3, 74 | |||
| 2, 35 | 2, 53 | 2, 86 | 3, 18 | 3, 40 | 3, 77 | |||
| 2, 41 | 2, 62 | 2, 88 | 3, 20 | 3, 46 | 3, 83 | |||
| 2, 47 | 2, 69 | 2, 90 | 3, 22 | 3, 53 | 3, 90 | |||
| 2, 52 | 2, 75 | 2, 91 | 3, 24 | 3, 61 | 3, 98 | |||
| 2, 56 | 2, 81 | 2, 93 | 3, 26 | 3, 73 | 4, 09 | |||
| 2, 60 | 2, 86 | 2, 94 | 3, 28 | 3, 80 | 4, 17 | |||
| 2, 64 | 2, 90 | 2, 96 | 3, 29 | 3, 87 | 4, 24 | |||
| 2, 67 | 2, 94 | 3, 02 | 3.36 | 3, 92 | 4, 28 | |||
| 2, 70 | 2, 98 | 3, 08 | 3, 42 | 3, 96 | 4, 32 | |||
| 2, 73 | 3, 02 | 3, 12 | 3, 48 | 3, 99 | 4, 35 | |||
| 2, 75 | 3, 05 | 3, 16 | 3, 52 | 4, 02 | 4, 38 | |||
| 2, 78 | 3, 08 | 3, 22 | 3, 58 | 4, 05 | 4, 41 |
Примечание. Значение исключается из ряда при > 0, 05 или  0, 01.
0, 01.
Если в указанной формуле среднее значение и коэффициент варьирования выводятся при исключении сомнительной варианты, тогда полученное значениесравнивается с критическим по критерию Стьюдента (табл.4.4). Число степеней свободы  берется равным п– 1.
берется равным п– 1.
Таблица 4.4
Критические значения критерия Стьюдента при Р0, 95и Р0, 99
| Р0, 95 | Р0, 99 | Р0, 95 | Р0, 99 | Р0, 95 | Р0, 99 | |||
| 2, 45 | 3, 71 | 2, 08 | 2, 83 | 2, 00 | 3, 65 | |||
| 2, 36 | 3, 50 | 2, 07 | 2, 82 | 1, 99 | 2, 64 | |||
| 2, 31 | 3, 36 | 2, 07 | 2, 81 | 1, 98 | 2, 64 | |||
| 2, 26 | 3, 25 | 2, 06 | 2, 80 | 1, 98 | 2, 63 | |||
| 2, 23 | 3, 17 | 2, 06 | 2, 79 | 1, 98 | 2, 62 | |||
| 2, 20 | 3, 11 | 2, 06 | 2, 78 | 1, 98 | 2, 61 | |||
| 2, 18 | 3, 06 | 2, 05 | 2, 77 | 1, 97 | 2, 60 | |||
| 2, 16 | 3, 01 | 2, 05 | 2, 76 | 1, 97 | 2, 60 | |||
| 2, 14 | 2, 98 | 2, 04 | 2, 76 | 1, 96 | 2, 59 | |||
| 2, 13 | 2, 95 | 2, 04 | 2, 75 | 1, 96 | 2, 59 | |||
| 2, 12 | 2, 92 | 2, 03 | 2.73 | 1, 96 | 2, 58 | |||
| 2, 11 | 2, 90 | 2, 02 | 2, 70 | 1, 96 | 2, 58 | |||
| 2, 10 | 2, 88 | 2, 01 | 2, 68 | 1, 96 | 2, 58 | |||
| 2, 09 | 2, 86 | 2, 01 | 2, 68 | 1, 96 | 2, 58 | |||
| 2, 09 | 2, 84 | 2, 00 | 2, 66 | 1, 96 | 2, 58 |
Примечание. Значение исключается из ряда при > 0, 05или0, 01.
Пример. Вычислимиз данных предыдущего примера (измерения длины побегов) при исключении сомнительной варианты:
= I3, 7 – 5, 6 I/ 0, 28 = 6, 79.
Полученное значение указывает, что первая варианта превосходит табличные значения критерия Стьюдента, а потому не должна включаться в данный ряд.
По каждому вариационному ряду выводятся показатели: среднее значение с ошибкой, среднее квадратичное отклонение с основной ошибкой (характеризует степень рассеянности ряда), коэффициент изменчивости (применительно к древостою, по А.В. Тюрину: до 10 % – малая изменчивость, 10-30 % –средняя и свыше 30 % – большая, по И.В. Семечкину: до 5 % – слабая, 6-10 % – умеренная, 11- 20 % – значительная, 21-50 % – большая, более 50 % – очень большая), точность опыта (показывает процент расхождения между средними значениями генеральной и выборочной совокупностей).