
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дисперсионный анализ. Задачей дисперсионного анализа является оценка влияния одного или нескольких факторов, а также их сочетаний на исследуемый признак
|
|
Задачей дисперсионного анализа является оценка влияния одного или нескольких факторов, а также их сочетаний на исследуемый признак. Различают одно-, двух- и многофакторный анализ. Также применяют ранговый дисперсионный анализ.
В лесохозяйственной практике наиболее часто используют одно- и двухфакторный дисперсионный анализ.
Для обработки и анализа формируется дисперсионный комплекс в виде таблицы, в которой исходные данные объединяют в градации для выявления действия факторов на результативный признак. При этом производят расчет факториальных, случайных и общих факторов. В качестве примера ниже приводятся расчеты однофакторного анализа по установлению степени и достоверности влияния возраста деревьев на их высоту. Начинается расчет с заполнения таблицы (табл. 4.12).
Таблица 4.12
Таблица для вычисления дисперсии между возрастом и высотой деревьев
| Гра- дации фактора (А, лет) | Результативный признак (высота, м), y | Число пов- торе- ний, п | ∑ у | 
| -уо* () | 2 | 2 п | ∑ (у-)2 |
| 4; 5; 4; 6 | 4, 8 | -13, 3 | 176, 9 | 707, 6 | 2, 76** | |||
| 18; 16; 15; 19; 17; 20 | 17, 5 | -0, 6 | 0, 4 | 2, 4 | 17, 50 | |||
| 22; 24; 19; 21; 22; 23 | 21, 8 | 3, 7 | 13, 7 | 82, 2 | 14, 84 | |||
| 24; 25; 27; 25; 24 | 25, 0 | 6, 9 | 47, 6 | 238, 0 | 6, 00 | |||
| Итого | 1030, 2 | 41, 1 | ||||||
* Средняя высота у0 =  = 18, 1 (м).
** (4-4, 8)2+(5-4, 8)2+(4-4, 8)2+(6-4, 8)2 = 2, 76. = 18, 1 (м).
** (4-4, 8)2+(5-4, 8)2+(4-4, 8)2+(6-4, 8)2 = 2, 76.
|
Факториальная (межгрупповая) дисперсия Дф= 1030, 2.
Случайная (внутригрупповая) дисперсия Дс= 41, 1.
Общая дисперсия До= Дф + Дс= 1030, 2 + 41, 1 = 1071, 3.
Показатель силы влияния 2:
2 =  =
=  = 0, 96.
= 0, 96.
Значение показателя силы влияния указывает очень сильную зависимость высоты деревьев от возраста. Факторы, определяющие увеличение высоты деревьев от возраста, составляют в примере 96 %.
Показатель достоверности влияния определяется по формуле (критерий Фишера)
F = 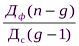 ,
,
где g – число градаций (для определения числа степеней свободы).
F = 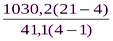 =
= 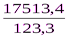 = 142, 0.
= 142, 0.
Сравнение со стандартным значением критерия Фишера при 5- и 1-процентном уровне значимости указывает на его достоверность, т.е. зависимость высоты деревьев от возраста свойственна всей генеральной совокупности, а не только частной выборке из 21 дерева.
Ошибка силы влияния равна:
m = ± (1-)  = ± (1-0, 96)
= ± (1-0, 96)  =±0, 007.
=±0, 007.
2 = 0, 96 ± 0, 007.