
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кп21. 593007. 201пз
|
|
Руководитель (А.А. Овчинникова)
Учащийся гр. 21593 (В.В. Зенчик)
Содержание:
Введение………………………………………………………………………………………….4
1. Анализ линейных и нелинейных электрических цепей постоянного тока………………..6
1.1. Расчет линейных электрических цепей постоянного тока…………………………….....6
1.2. Расчет нелинейных электрических цепей постоянного тока…………………………...19
2. Анализ электрического состояния линейных электрических цепей переменного тока: однофазных, трехфазных. Исследование переходных процессов в электрических цепях…..
2.1. Расчет однофазных линейных электрических цепей переменного тока………………….
2.2. Расчет трехфазных линейных электрических цепей переменного тока………………….
2.3. Исследование переходных процессов в электрических цепях…………………………….
Заключение…………………………………………………………………………………….......
Список используемой литературы……………………………………………….........................
Приложение 1.Потенциальная диаграмма………………………………………………………
Приложение 2.Вольт-амперные характеристики линейных и нелинейных элементов……....
Введение
Электрической цепью называют совокупность соединённых друг с другом источников электрической энергии и нагрузок, по которым может протекать электрический ток. Электромагнитные процессы в электрической цепи можно описать с помощью понятий «ток», «напряжение», «ЭДС», «сопротивление».
Постоянным током называют ток, неизменный во времени. Его принято обозначать буквой I, ЭДС источника – Е, сопротивление – R. В международной системе единиц (СИ) единица тока – ампер (А), единица ЭДС – вольт (В), единица сопротивление – ом (Ом).
Изображение электрической цепи с помощью условных знаков называют электрической схемой.
Зависимость тока, протекающего по сопротивлению, от напряжения на этом сопротивлении называют вольт-амперной характеристикой (ВАХ). По оси абсцисс на графике обычно откладывают напряжение, по оси ординат – ток.
Сопротивления, ВАХ которых являются прямыми линиями называют линейными, электрические цепи только с линейными сопротивлениями – линейными электрическими цепями.
Сопротивления, ВАХ которых не являются прямыми линиями, т.е. они нелинейны, называют нелинейными, аэлектрические цепи с нелинейными сопротивлениями – нелинейнымиэлектрическимицепями.
Источник электрической энергии характеризуется ЭДС E и внутренним сопротивлением r. Источник ЭДС представляет собой такой источник питания, напряжение на зажимах которого постоянно и равно ЭДС E, а внутреннее сопротивление равно нулю.
Электрические цепи подразделяют на неразветвленные и разветвленные. В неразветвленной цепи во всех элементах ее течёт один и тот же ток. В разветвлённой же цепи, в каждой ветви ее течёт свой ток. Ветвь можно определить, как участок цепи, образованный последовательно соединёнными элементами (через которые течет одинаковый ток) и заключенный между двумя узлами. В свою очередь, узел – это точка цепи, в которой сходятся не менее трёх ветвей.
Под напряжением на некотором участке электрической цепи понимают разность потенциалов между крайними точками этого участка.
В электротехнике разность потенциалов на концах сопротивления называют либо напряжениемнасопротивлении, либо падениемнапряжения (произведение IR)
Все электрические цепи подчиняются первому и второму законам Кирхгофа.
Первый закон Кирхгофа можно сформулировать двояко:
1) алгебраическаясумматоков, подтекающихклюбомуузлусхемы, равнанулю;
2) суммаподтекающихк любому узлу токов равна сумме утекающих от узла токов.
Согласно первой формулировке I1-I2-I3-I4=0,
согласно второй – I1=I2+I3+I4.
Физически, первый закон Кирхгофа означает, что движение зарядов в цепи происходит так, что ни в одном из узлов они не скапливаются.
Второй закон Кирхгофа также можно сформулировать двояко:
1) алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура:
∑ IR=∑ E
2) алгебраическая сумма напряжений вдоль любого замкнутого контура равна нулю:
∑ Ukl= 0
Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений. Законы Кирхгофа используются для нахождения токов в ветвях схемы.
При протекании токов по сопротивлениям в последних выделяется теплота. На основании закона сохранения энергии количество теплоты, выделяющееся в единицу времени в сопротивлениях схемы, должно равняться энергии, доставляемой за то же время источником питания. Уравнение энергетического баланса при питании только от источников ЭДС имеет вид
∑ EI=∑ I2R.
Под потенциальной диаграммойпонимают график распределения потенциала вдоль какого-либо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с какой-либо произвольной точки, по оси ординат – потенциалы. Каждой точке участка цепи или замкнутого контура соответствует своя точка на потенциальной диаграмме.
При расчёте методом контурных токовполагают, что в каждом независимом контуре схемы течет свой контурный ток. Уравнения составляют относительно контурных токов, после чего через них определяют токи ветвей.
1.1. РАСЧЁТ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Для электрической цепи, изображенной на рис. 1 выполнить следующее:
1) Определить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы;
2) Определить токи во всех ветвях схемы, используя метод контурных токов;
3) Определить токи во всех ветвях схемы на основании метода наложения;
4) Составить баланс мощностей для заданной схемы;
5) Результаты расчетов токов по пунктам 2 и 3 представить в виде таблицы и сравнить;
6) Определить ток во второй ветви методом эквивалентного генератора;
7) Построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.
| E2, r02 |
| I3 |
| А |
| А’ |
| C |
| C’ |
| D |
| R1 |
| R3 |
| R5 |
| R4 |
| R6 |
| E1, r01 |
| I5 |
| R2 |
| I1 |
| I2 |
| I4 |
| Iк1 |
| Iк2 |
| Iк3 |
Дано: E1=20(В); Е2=30(В); R1=64(Ом); R2=43(Ом); R3=31(Ом); R4=25(Ом); R5=52(Ом); R6=14(Ом); r01=1(Ом); r02=2(Ом).
Рис. 1
1) Составить систему уравнений, применяя законы Кирхгофа для определения токов во всех ветвях.
Метод узловых и контурных уравнений основан на применении первого и второй законов Кирхгофа. Он не требует никаких преобразований схемы и пригоден для расчёта любой цепи.
При расчёте данным методом произвольно задаем направление токов в ветвях I1, I2, I3, I4, I5.
Составляем систему уравнений. В системе должно быть шесть уравнений. Сначала составляем уравнения для узлов по первому закону Кирхгофа. Для цепи с n узлами можно составить (n-1) независимых уравнений. В нашей цепи четыре узла, значит число уравнений: n -1=3-1=2.
Составляем три уравнения для любых 2-х узлов.
0=I2+I3-I1-I5; 0=-I4+I5-I2.
Всего в системе должно быть пять уравнений. Два уже есть. Составляем три недостающих и объединяем все уравнения в систему:
0=I2+I3-I1-I5
0=-I4+I5-I2
E1=I1 (R1+r01) +I3 (R3+R6)
E1+E2=I2 (R2+r02) + I1 (R1-r01) - I4R4
E2=I2 (R2+r02) + I5R5
Решив систему, определим величину и направление тока во всех ветвях схемы.
Подставив в числовые значения, имеем:
0=I2+I3-I1-I5
0=-I4+I5-I2
20=I1*65+I3*45
50=I2* 45 + I1*65 - I4*25
30=I2 *45 + I5*52
Решим систему с помощью определителей. Вычислим определитель системы ∆ и частные определители ∆ 1, ∆ 2, ∆ 3, ∆ 4, ∆ 5, ∆ 6.
| -1 | -1 | ||||||
| -1 | -1 | ||||||
 = =
| = | -807875 | |||||
| -25 | |||||||
| -1 | |||||||
| -1 | -1 | ||||||
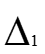 = =
| = | -252800 | |||||
| -25 | |||||||
| -1 | -1 | ||||||
| -1 | |||||||
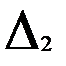 = =
| = | -388650 | |||||
| -25 | |||||||
| -1 | -1 | ||||||
| -1 | -1 | ||||||
 = =
| = | ||||||
| -25 | |||||||
| -1 | -1 | ||||||
| -1 | |||||||
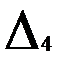 = =
| = | ||||||
| -1 | |||||||
| -1 | -1 | ||||||
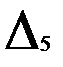 = =
| = | -129750 | |||||
| -25 | |||||||
Вычисляем действительные токи ветвей:
I1= 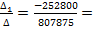 0.3129 (А)
0.3129 (А)
I2= 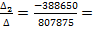 0.4811 (А)
0.4811 (А)
I3= 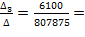 -0.0076 (А)
-0.0076 (А)
I4= 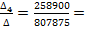 -0.3205 (А)
-0.3205 (А)
I5= 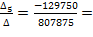 0.1606 (А)
0.1606 (А)
2) Определить токи во всех ветвях схемы, используя метод контурных токов.
Метод контурных токов основан на использовании только второй закона Кирхгофа. Это позволяет уменьшить число уравнений в системе на n -1.
Достигается это разделением схемы на независимые контуры и введением для каждого контура своего тока – контурного тока, являющегося расчётной величиной.
Итак, в заданной цепи (рис. 1) можно рассмотреть три контура (ACA’A, АА’СC’ДА, ДC’CД) и ввести для них контурные токи Iк1, Iк2, Iк3.
При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур, в правой части равенства алгебраически суммируются напряжения на сопротивлениях, входящих в этот контур, а также учитывается падение напряжения на сопротивлениях смежной ветви, определяемое по контурному току соседнего контура.
На основании вышеизложенного порядок расчёта цепи методов контурных токов будет следующим:
стрелками указываем выбранные направления контурных токов Iк1, Iк2, Iк3 в контурах. Направление обхода контуров принимаем таким же;
составляем уравнения и решаем систему уравнений.
E1=Iк1 (R1+r01+R3+R6) +Iк2 (R1+r01)
E2+E1=Iк2 (R01+R1+R4+R2+r02) +Iк1 (R1+r01) +Iк3 (r02+R2)
E2=Iк3 (R2+r02+R5) +Iк2 (R2+r02)
Подставляем в уравнение численные значения ЭДС и сопротивлений.
20=111Iк1+65Iк2
50=135Iк2+65Iк1+45Iк3
30=97Iк3+45Iк2
Решим систему с помощью определителей. Вычислим определитель системы ∆ и частные определители ∆ 1, ∆ 2, ∆ 3.
 = =
| = | ||||
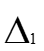 = =
| = | -6100 | |||
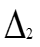 = =
| = | ||||
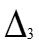 = =
| = | ||||
Вычисляем контурные токи:
Iк1= 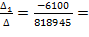 -0.0074 А; Iк2=
-0.0074 А; Iк2= 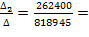 0.3204 А; Iк3=
0.3204 А; Iк3=  0.1606 А;
0.1606 А;
Действительные токи ветвей:
I1=-Iк1+Iк2=0.313 А,
I2=Iк2+Iк3=0.481 А,
I3=Iк1=0.007 А,
I4=Iк2=0.320 А,
I5=-Iк3=0.1606 А.
3) Определить токи во всех ветвях схемы на основании метода наложения.
По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности.
a) Определяем частные токи от ЭДС Е1, при отсутствии ЭДС Е2, т.е. рассчитываем цепь по рис. 2.
Показываем направление частных токов от ЭДС Е1 и обозначаем буквой I с одним штрихом (I’).
| E2, r02 |
| I3 |
| А |
| А’ |
| C |
| C’ |
| D |
| R1 |
| R3 |
| R5 |
| R4 |
| R6 |
| E1, r01 |
| I5 |
| R2 |
| I1 |
| I2 |
| I4 |
| Iк1 |
| Iк2 |
| Iк3 |
R02, 2= R02+R2 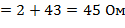 ;
;
R022, 5 = 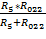 =
= 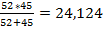 Ом;
Ом;
R0225, 4 =R4+R0225 = 25+24, 124=49, 124 Ом;
R3, 6 =R3+R6= 31+14= 45 Ом;
R02254, 36 = 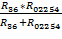 =
=  23, 5 Ом;
23, 5 Ом;
Rэкв=R1+R01+R0225436=64+1+23, 5 = 88, 5 Ом;
Ток источника
I1’= 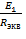 =
= 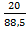 = 0, 226 А
= 0, 226 А
Вычисляем токи ветвей
I3’= 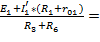
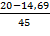 =
= 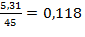 A;
A;
I4’=I1’-I3’= 0, 226-0, 118 = 0, 108 A;
I2’= 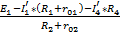 =
= 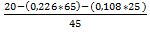 = 0, 058 A;
= 0, 058 A;
I5’=I4 - I2’= 0, 108-0, 058 = 0, 05 A;
Составляем баланс мощностей для проверки:
E1*I1’=I1’2(r01+R1) +I2’2*(r02+R2) +I3’2*R3+ I4’2*R4+ I5’2*R5, откуда
4, 52(Вт)≈ 4, 26(Вт)
b) Определяем частные токи от ЭДС Е2 при отсутствии ЭДС Е1, т.е. рассчитываем простую цепь по рис.3.
Показываем направление частных токов от ЭДС Е2 и обозначаем буквой I с двумя штрихами (I’’).
Рассчитываем общее сопротивление цепи:
| E2, r02 |
| I3 |
| А |
| А’ |
| C |
| C’ |
| D |
| R1 |
| R3 |
| R5 |
| R4 |
| R6 |
| E1, r01 |
| I5 |
| R2 |
| I1 |
| I2 |
| I4 |
| Iк1 |
| Iк2 |
| Iк3 |
R01, 1= R01+R1 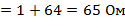 ;
;
R3, 6 =R3+R6= 31+14= 45 Ом;
R011, 36 = 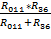 =
= 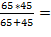 26, 6 Ом;
26, 6 Ом;
R01136, 4= R01136+R4 = 26, 6 + 25 = 51, 6 Ом; R011364, 5= 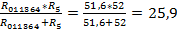 Ом
Ом
Rэкв= R2+R02+R0113645= 45+25, 9 = 70, 9 Ом
Вычисляем ток источника
I2”= 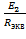 =
= 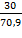 = 0.423 А
= 0.423 А
Вычисляем токи ветвей
I5”=  0.210 А;
0.210 А;
I4”= I2”-I5”= 0, 423-0, 210 = 0, 213 А;
I1”= 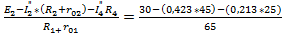 0.086 А;
0.086 А;
I3”= I4”-I1”=0, 231-0, 086= 0, 127 А;
Составляем баланс мощностей для проверки:
E2*I2”=I1”2(r01+R1) +I2”2*(R02+R2) + I3”2*R3+ I4”2*R4+ I5”2*R5
12, 69(Вт)≈ 12, 46(Вт)
Вычисляем токи ветвей исходной цепи (рис. 1), выполняя алгебраическое сложение частных токов, учитывая их направление:
I1= I1’-I1”=0.244 А; I2= I2’-I2”=-0.220 А; I3= I3’+I3”=0.465 А;
I4= I4’-I4”=0.197 А; I5= I5’-I5”=0.047 А; I6= I6’-I6”=0.268 А.
4) Составить баланс мощностей для заданной схемы.
Источники Е1 и Е2 вырабатывают электрическую энергию, т.к. направление ЭДС и тока в ветвях с источниками совпадают. Баланс мощностей для заданной цепи запишется так:
Е1*I2+ E2*I2=I12(r01+R1) +I22*(R2+r02) + I32*R3+I42*R4+ I52*R5, откуда
16.39 Вт= 16.29 Вт.
С учётом погрешности расчётов баланс мощностей получился.
5) Результаты расчётов токов по пунктам 2 и 3 представить в виде таблицы и сравнить.
| Ток в ветви Метод расчёта | I1, А | I2, А | I3, А | I4, А | I5, А | I6, А |
| Метод контурных токов Метод наложения | 0, 244 0, 244 | 0, 220 0, 220 | 0, 465 0, 465 | 0, 197 0, 197 | 0, 047 0, 047 | 0, 268 0, 268 |
Расчёт токов ветвей обоими методами с учётом ошибок вычислений одинаков.
6) Определить ток во второй ветви методом эквивалентного генератора.
Метод эквивалентного генератора используется для исследования работы какого-либо участка в сложной электрической цепи.
Изображаем схему эквивалентного генератора в режиме холостого хода (рис. 4), т.е. при отключенном потребителе R2 от зажимов, а и б. В этой схеме есть контур, в котором течет ток режима холостого хода. Определим его величину:
| E2, r02 |
| I3 |
| А |
| А’ |
| C |
| C’ |
| D |
| R1 |
| R3 |
| R5 |
| R4 |
| R6 |
| E1, r01 |
| I5 |
| I1 |
| I2 |
| I4 |
| Iхх |
| + |
| - |
| а |
| б |
Iхх= 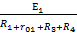 =0.303 А
=0.303 А
Найдём Uхх:
Uхх=Iхх (R3+R4) – E2=5.75 В.
Вычисляем ток в исследуемой ветви:
I2=  =0.220 А.
=0.220 А.
7) Построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.
Возьмем контур АА’CДEA. Зададимся обходом контура против часовой стрелки. Заземлим одну из точек контура, пусть это будет точка A. Потенциал этой точки равен нулю φ A=0 (рис. 1).
Зная величину и направление токов ветвей и ЭДС, а также величины сопротивлений, вычислим потенциалы всех точек контура при переходе от элемента к элементу. Начнём обход от точки A.
φ Д= φ Е+E2-I2*r02=29.558 B;
φ C= φ Д-I5*R5=32.364 B;
φ А’= φ С-Е1+I1*r01=-7.393 B;
φ А= φ А’+I1*R1=5.243 B;
φ E= φ A-I2*R2=0 – проверочная точка.
Строим потенциальную диаграмму. По оси абсцисс откладываем сопротивления контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, по оси ординат – потенциалы точек с учетом их знака. Потенциальная диаграмма представлена на листе Приложение 1.
1.2. РАСЧЁТ НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
| |
| нэ1 |
| R3 |
| нэ2 |
| Рис. 5 |
| + |
| - |
| U |
Дано: U=60 B, R3=40 Ом.
Расчёт цепи производим графическим методом. Для этого в общей системе координат строим вольтамперные характеристики линейного и нелинейных элементов.
ВАХ линейного элемента строим по уравнению I=UR/R. Она представляет собой прямую, проходящую через начало координат. Для определения координаты второй точки ВАХ линейного элемента задаемся произвольным значением напряжения. Например, UR=200 B, тогда соответствующее значение тока I3=UR/R3=200/40=5 A. Соединив полученную точку с началом координат, получим ВАХ линейного элемента. Далее строится общая ВАХ цепи с учётом схемы соединения элементов. В нашей цепи соединение элементов смешанное. Поэтому графически «сворачиваем» цепь. Начинаем с разветвлённого участка. Нелинейные элементы соединены последовательно, их ВАХ I1=f(U1) и I2=f(U2). С учётом этого строим общую для них ВАХ. Для этого задаёмся током и складываем напряжения U3=U1+U2. Точка пересечений этих значений напряжения и тока даёт одну из точек их общей ВАХ. В результате получаем множество точке и по ним строим ВАХ I3=f(U12).
Далее мы имеем характеристики линейного элемента I3=f(U3) и нелинейного элемента (нэ12) I3=f(U12), которые соединены между собой параллельно. Строим для них общую ВАХ. В данном случае задаёмся напряжение и складываем токи. Проделываем это многократно. По полученным точка строим общую ВАХ цепи I3=f(U).
Дальнейший расчёт цепи производим по полученным графикам.
Чтобы найти токи и напряжения на всех элементах цепи, поступаем так: по оси напряжений находим значение напряжения, равное 60 В (точка «а»). Из этой точки восстанавливаем перпендикуляр до пересечения с общей ВАХ I3=f(U), получим точку «в». Из точки «в» опускаем перпендикуляр на ось тока (точка «с»). Отрезок «ос» дает нам искомое значение общего тока I3=1, 8 А. Когда опускаем перпендикуляр из точки «в» на ось тока, то пересекаем ВАХ I3=f(U3) и I3=f(U12) в точках «f» и «d» соответственно. Опуская перпендикуляры из этих точек на ось напряжения, получим напряжения на каждом участке цепи: U3=70 В и U12=253 В, откуда напряжение U2=180 В, а U1=73 В. Т.к. нелинейные элементы соединены последовательно, то I1=I2=I12=1.8 А. В результате имеем следующие значения токов и напряжений на всех элементах цепи: I1=1.8 A, I2=1.8 А, I3=1.8 А, U1=73 Вт, U2=180 Вт, U3=70 В.
Графики представлены на листе Приложение 2.