
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Доказательство. Евклидово пространство
|
|
Евклидово пространство
Определение 1. Линейное пространство L над полем действительных чисел называется евклидовым, если в нем введена функция, которая любой паре векторов 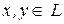 ставит в соответствие действительное число, называемое скалярным произведением, обозначаемое символом
ставит в соответствие действительное число, называемое скалярным произведением, обозначаемое символом 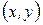 , и обладающая свойствами:
, и обладающая свойствами:
1) 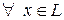 и
и 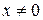
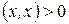 ;
;
2) 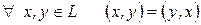 ;
;
3) 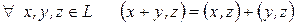 ;
;
4) 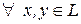 и
и 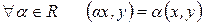 .
.
Обозначение. Евклидово пространство, чаще всего, обозначают: Е. Если размерность исходного линейного пространства равна n, то используют обозначение: 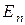 .
.
Для элементов евклидова пространства из свойств 1) - 4) автоматически следуют такие следствия.
Следствие 1. 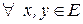 и
и 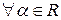
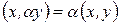 .
.
Доказательство.
.
Следствие 2. 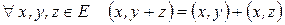 .
.
Доказательство.
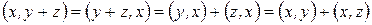 .
.
Следствие 3. 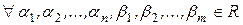 ,
, 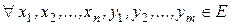
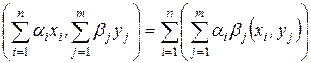 ,
, 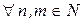 .
.
Доказательство.
Доказательство данного утверждения легко провести методом математической индукции. При 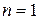 и
и 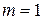 справедливость утверждения следует из свойств 3) - 4) и следствий 1 и 2. Предположим, что утверждение верно при
справедливость утверждения следует из свойств 3) - 4) и следствий 1 и 2. Предположим, что утверждение верно при 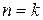 и
и 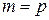 , т.е.
, т.е. 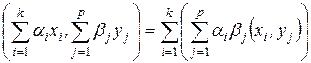 . Это означает, что утверждение будет верно и при всех
. Это означает, что утверждение будет верно и при всех 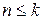 и
и 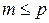 .
.
Покажем, что в этом случае оно остается справедливым и при 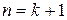 и
и 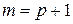 . Действительно,
. Действительно,
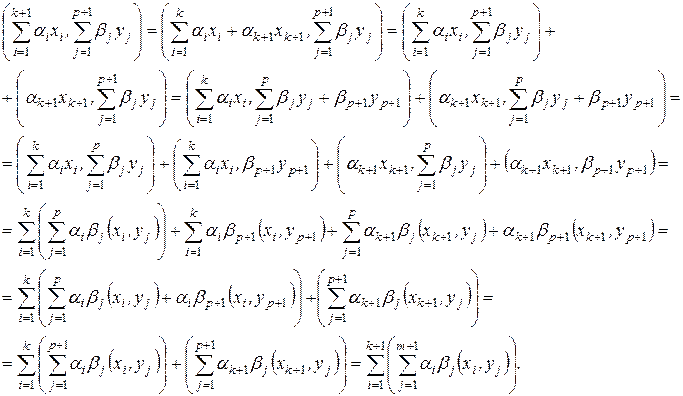
Следствие 4. 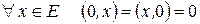 .
.
Доказательство.
Справедливость этого утверждения следует из свойства 4 при 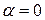 и свойства 2. Действительно,
и свойства 2. Действительно,
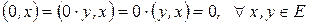 ;
;  .
.
Из следствия 4 следует, в частности, что 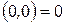 . А это означает автоматически справедливость следствия 5.
. А это означает автоматически справедливость следствия 5.
Следствие 5. 1) 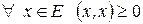 ;
;
2) 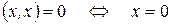 .
.
Теорема 1. Любое конечномерное линейное пространство L является евклидовым.
Доказательство.
Пусть 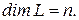 Зафиксируем в нем какой-нибудь базис
Зафиксируем в нем какой-нибудь базис 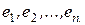
Для любых векторов 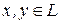 скалярное произведение
скалярное произведение 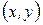 можно вести опираясь на координаты векторов в этом базисе:
можно вести опираясь на координаты векторов в этом базисе:
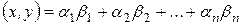 , где
, где 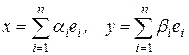 .
.
Справедливость выполнения свойств 1) – 4) проверьте самостоятельно.