Доказательство. Справедливость утверждения следует из свойств скалярного произведения.

Справедливость утверждения следует из свойств скалярного произведения.

Следствие. Если в конечномерном евклидовом пространстве 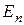задан ортонормированный базис 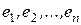, то для 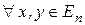, таких что

, .

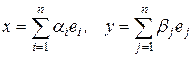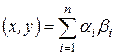Доказательство.

Справедливость утверждения следует из теоремы 6 и свойств ортонормированной системы векторов.

Теорема 7 (Критерий ортонормированности базиса в конечномерном евклидовом пространстве). Базис 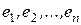евклидова пространства 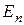- ортонормированный тогда и только тогда, когда для 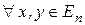, таких что

, .

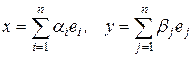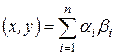Доказательство. Если базис - ортонормированный, то справедливость утверждения уже отмечена следствием к теореме 6. Следовательно, достаточно доказать, что если скалярное произведение векторов в евклидовом пространстве определяется по формуле: 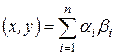, когда 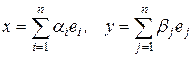, то базис 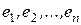- ортонормированный.

Заметим, что 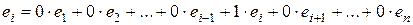, т.е. у вектора 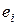координата 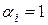, а остальные , ;

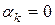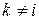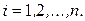
Аналогично, 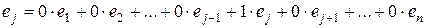, т.е. у вектора 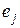координата 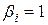, а остальные , ;

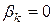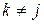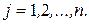
Из этого следует, что по указанному выше правилу определения скалярного произведения векторов 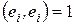, 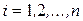; 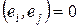, 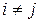. Таким образом, базис 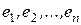- ортонормированный. Что и требовалось доказать.