Доказательство. Справедливость свойства 1) следует из свойств скалярного произведения, рассмотренных выше.

Справедливость свойства 1) следует из свойств скалярного произведения, рассмотренных выше.

Справедливость свойства 2) следует из неравенства Коши-Буняковского и свойств абсолютной величины действительного числа:

.

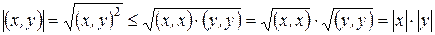Из свойства 2) следует, что 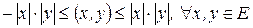. Это соотношение окажется полезным при доказательстве свойства 3.

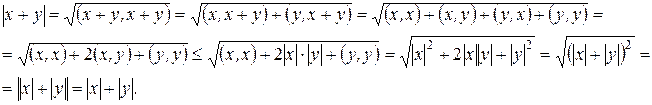
Таким образом, понятие длины, введенное в евклидовом пространстве, не противоречит ранее известному понятию длины из школьной программы.

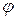Определение 3. Углом между векторами называется число , удовлетворяющее условию: .

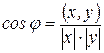Замечания. 1)Угол можно определить только для ненулевых векторов.

2) Формула не противоречит ранее известным свойствам функции : .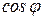

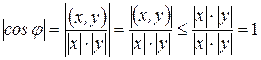Определение 4. Векторы называются ортогональными, если .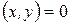

Обозначение: .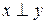

Замечание. Очевидно, что векторы ортогональны, тогда и только тогда, когда либо , либо один из векторов – нулевой.

Определение 5. Система векторов называется ортогональной, если векторы попарно ортогональны, т.е. .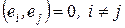

Определение 6. Система векторов называется ортонормированной, если векторы попарно ортогональны и длина каждого равна 1, т.е.

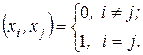
Замечание. Ортонормированная система векторов не может содержать нулевой вектор.

Теорема 4. Если система векторов - ортонормированная, то она является линейно независимой.