Доказательство. и , т.е. неравенство остается справедливым.

1) Пусть 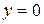. Тогда

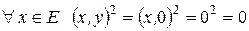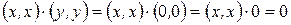и , т.е. неравенство остается справедливым.

2) Пусть 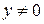. Тогда, для 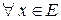и 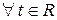из свойств скалярного произведения (и следствий к ним) следует, что .

В тоже время,

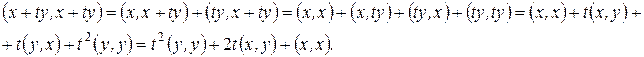Это означает, что .

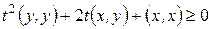Нетрудно заметить, что выражение в левой части данного неравенства представляет собой квадратный трехчлен относительно переменной t, причем, для рассматриваемой ситуации (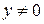), старший коэффициент 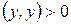. Следовательно, ветви графика соответствующей параболы направлены вверх. В этом случае квадратный трехчлен принимает неотрицательные значения при всех значениях t лишь в том случае, когда дискриминант квадратного трехчлена .

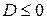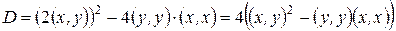, следовательно,

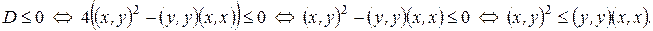Что и требовалось доказать.

Определение 2. Длиной вектора 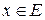называется число .

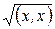Обозначение: .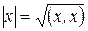

Теорема 3 (свойства длины). 1) 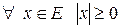, причем, ;

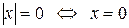2) ;

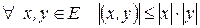3) .