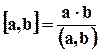Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример. Модулярная арифметика. Основные свойства
|
|
Лабораторная работа №1
Модулярная арифметика. Основные свойства
Цель работы: изучение основных свойств сравнений по модулю n
Теоретические сведения
Основные понятия арифметики целых чисел
В криптографии нас интересуют операции в приложении к множеству целых чисел.
Множество целых чисел обозначается символом Z. Целыми числами являются {..., –2, –3, 0, +1, +2,...}
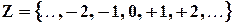
Символом N – множество натуральных чисел. Натуральными числами являются {1, 2, 3, …}.
Необходимо заметить, что 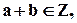
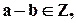
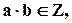 (для любых)
(для любых) 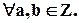 Т.е. сумма, разность и произведение двух целых чисел a и b будут также целыми.
Т.е. сумма, разность и произведение двух целых чисел a и b будут также целыми.
Определение 1.1. Пусть а, b – элементы из Z, b ≠ 0. Число b делит a (записывают b | a либо а 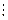 b), если существует такое целое c, что a=bс.
b), если существует такое целое c, что a=bс.
Синонимы: a кратно b, b делитель a.
Но частное от деления a на b (если b не равно нулю) не всегда является целым числом.
Теорема 1.1. Пусть а – целое, b – натуральное. Тогда существуют такие однозначно определённые q, r Î Z, 0 ≤ r < b, что
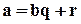 (1)
(1)
Определение 1.2. Число q называется неполным частным, а число r – остатком от деления a на b.
Пример.
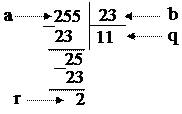 |
Предположим, что а=255, b= 23. Найдем q и r. (см. рис.)
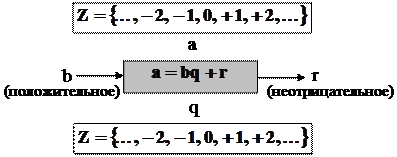 |
Необходимо обратить внимание на два ограничения, которые налагаются на b и r, согласно теореме 1.1. (см. рис)
Справедливы следующие свойства теории делимости.
Свойство 1.1. b | a, b | с, следовательно (Þ)b | ma± nс, где m, nÎ Z.
Свойство 1.2. b | a и a | c, следовательноb | с.
Свойство 1.3. b | a, a | b тогда и только тогда, когда (Û)b= ±a.
 |
Два целых числа могут иметь много делителей, но только один наибольший общий делитель. Например, общие делители чисел 12 и 140 есть 1, 2 и 4. Однако наибольший общий делитель — 4 (см. Рис)
Определение 1.3. Целое число d, делящее одновременно числа 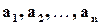 Î Z, называется их общим делителем.
Î Z, называется их общим делителем.
Определение 1.4. Наибольший из всех общих делителей чисел 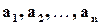 называется их наибольшим общим делителем (НОД) и обозначается НОД
называется их наибольшим общим делителем (НОД) и обозначается НОД 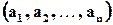 или
или 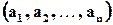 .
.
Далее будем рассматривать лишь положительные делители чисел.
Рассмотрим НОД двух чисел.
Теорема 1.2. Если b|a 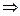 совокупность общих делителей a и b совпадает с совокупностью делителей b. В частности, (a, b)=b.
совокупность общих делителей a и b совпадает с совокупностью делителей b. В частности, (a, b)=b.
Теорема 1.3. Если a=bq+c, то совокупность общих делителей a и b совпадает с совокупностью общих делителей b и c. В частности, (a, b)=(b, c)
Теорема 1.4. Если (a, b) =d, то найдутся такие целые числа u и v, что d=au + bv.
Для поиска наибольшего общего делителя применяется алгоритм Эвклида. Последний состоит в ниже следующем.
Пусть a и b – положительные целые. Считаем что a> b. В алгоритме используются два факта, основанные на теоремах 1.2 и 1.3.
Факт 1. НОД (a, 0) = a.
Факт 2: НОД (a, b) = НОД (b, r), где r – остаток от деления a на b.
Тогда в силу теоремы делимости (формула 1) находим ряд равенств:
a=bq1+r1, 0< r1< b
b=r1q2+r2, 0< r2< r1
r1=r2q3+r3, 0< r3< r2
...…………………
rn-3=rn-2qn-1+rn-1, 0< rn-1< rn-2
rn-2=rn-1qn+rn, 0< rn< rn-1
rn–1=rnqn+1 +rn+1.
Заканчивающийся, когда получаем некоторое rn+1=0. Последнее неизбежно, т.к. ряд b, r1, r2, …. – ряд убывающих целых чисел (b> r1> r2> …), который не может содержать более b положительных чисел.
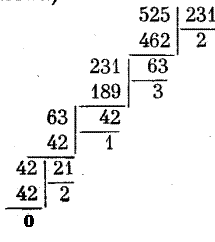 Пример. Применим алгоритм Эвклида к отысканию НОД(525, 231). Вспомогательные вычисления приведены на рис.
Пример. Применим алгоритм Эвклида к отысканию НОД(525, 231). Вспомогательные вычисления приведены на рис.
Тоже самое вычисление в виде цепочки неравенств.
525 = 231 · 2 + 63
231 = 63 · 3 + 42
63 = 42 · 1 + 21
42 = 21 · 2 +0
Таким образом (525, 231) = 21.
Алгоритм Эвклида дает практический способ нахождения чисел u и v из теоремы 1.4. из цепочки равенств имеем:
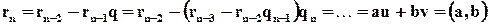
(идем по цепочке равенств снизу вверх, выражая из каждого следующего равенства остаток и подставляя его в получившееся уже к этому моменту выражение). Т.о. получаем линейное представление наибольшего общего делителя, используя расширенный алгоритм Эвклида.
Для предыдущего примера получаем линейное представление наибольшего общего делителя:
21 = 63 – 42 · 1 = 63 – (231 – 63 · 3) · 1 =
=63 – (231 – (525– 231 · 2) · 3) · 1=
= 525– 231 · 2 – (231 – (525– 231 · 2) · 3) =
=525–231 · 2 –231+(525– 231 · 2) · 3=
=525–231 · 2 –231+525· 3– 231 · 2· 3=
=525· 4–231· 9,
и согласно теореме 1.4. u=4 и v= – 9.
Представление наибольшего общего делителя, используя расширенный алгоритм Эвклида, можно представить в виде таблицы
| № | a | b | a mod b | 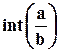
| d | u | v |
| –9 | |||||||
| –1 | |||||||
| –1 | |||||||
| – | – |
В первых пяти столбцах (движение алгоритма вниз) – обычный алгоритм Эвклида.
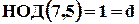
Здесь 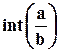 – целая часть при делении a на b;
– целая часть при делении a на b;
a mod b – остаток от деления a на b;
d – НОД(a, a);
И по теореме 1.4., если (a, b) =d, то найдутся такие целые числа u и v, что d=au + bv.
Последние два столбца (движение вверх) дают нам рекурсию построения расширенного алгоритма Эвклида.
Из последней (пятой) строки, используя d=au + bv, записываем
21× u + 0× v= 21.
Следовательно, u=1, v=0. Заполняем нижнюю строку таблицы в двух последних столбцах.
Далее все время пользуемся au + bv=21  и
и 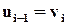 , поднимаясь вверх по таблице.
, поднимаясь вверх по таблице.
Для четвертой строки таблицы  и
и 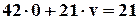 , следовательно v=1.
, следовательно v=1.
И т.д.
Определение 1.5. Если 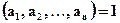 , то
, то 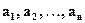 называются взаимно простыми.
называются взаимно простыми.
Определение 1.6. Если 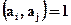 ,
, 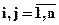 ,
, 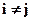 , то числа
, то числа 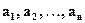 называются попарно простыми.
называются попарно простыми.
Утверждение. Если числа 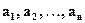 – попарно простые, то они взаимно простые.
– попарно простые, то они взаимно простые.
Пример. Определим, являются ли числа 27, 69 и 23 взаимно простыми и попарно простыми.
НОД(27, 69)=3, НОД(69, 23)=23, НОД(27, 23)=1. Числа не являются попарно простыми.
НОД(27, 69, 23)=1. Числа являются взаимно простыми.
Определение 1.7. Если a1|b, a2|b, …, an|b, то b Î Z называется общим кратным чисел a1, …, an Î Z.
Определение 1.8. Наименьшее положительное общее кратное чисел a1, …, an называется их наименьшим общим кратным (НОК).
Наименьшее общее кратное принято обозначать 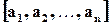 .
.
Рассмотрим НОК двух чисел.
Теорема 1.5. Общие кратные двух чисел совпадают с кратными их общего наименьшего кратного. т.е. если М – общее кратное целых а, b, то 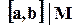 .
.
Теорема 1.6. Общее наименьшее кратное двух чисел рано их произведению, деленному на их наибольший общий делитель