Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Аm º bm (mod n)º (b mod n) m mod n
|
|
Пример:
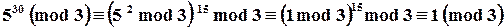
Пример:
Найти остаток от деления числа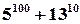 
на 11.
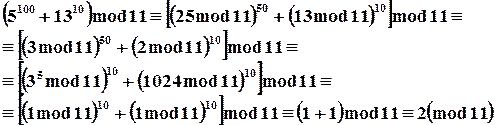
Криптография использует множество вычислений по модулю n, потому что задачи типа вычисления дискретных логарифмов и квадратных корней очень трудны. Кроме того, с вычислениями по модулю удобнее работать, потому что они ограничивают диапазон всех промежуточных величин и результата.
Для модуля n длиной k бит промежуточные результаты любого сложения, вычитания или умножения будут не длиннее 2k бит. Поэтому возведение в степень в модулярной арифметике можно выполнить без генерации очень больших промежуточных результатов.
Вычисление степени числа а по модулю n
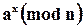
можно выполнить как ряд умножений и делений. Существуют способы сделать это быстрее. Поскольку эти операции дистрибутивны, быстрее произвести возведение в степень как ряд последовательных умножений, выполняя каждый раз приведение по модулю. Это особенно заметно, если работать с длинными числами (200 бит и более).
Например, если нужно вычислить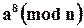 
,
не следует применять примитивный подход с выполнением семи перемножений и одного приведения по модулю громадного числа:
(а*а*а*а*а*а*а*а) mod n.
Вместо этого выполняют три малых умножения и три малых приведения по модулю:
((a2 mod n)2 mod n)2 mod n.
Тем же способом вычисляют
a16 mod n = (((a2 mod n)2 mod n)2 mod n)2 mod n.
Вычисление
,
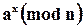где х не является степенью 2, лишь немного сложнее.
Двоичная запись числа х позволяет представить число х как сумму степеней 2:
х = 25(10) ®11 0 0 1(2), поэтому 25 = 24 + 23 + 20=16+8+1.
Тогда
a25 mod n = (а * a24) mod n = (а * а8 * a16) mod n = = а * ((а2)2)2 * (((a2)2)2)2 mod n = ((((а2 * а)2)2)2 * a) mod n.
При разумном накоплении промежуточных результатов потребуется только шесть умножений:
(((((((a2 mod n) * a) mod n)2 mod n)2 mod n)2 mod n) * a) mod n.
Этот метод уменьшает трудоемкость вычислений до 1, 5k операций в среднем, где k-длина числа в битах
Поскольку многие алгоритмы шифрования основаны на возведении в степень по модулю n, целесообразно использовать алгоритмы быстрого возведения в степень.
Пример
 |
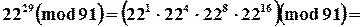
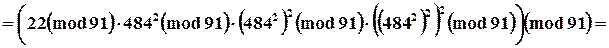
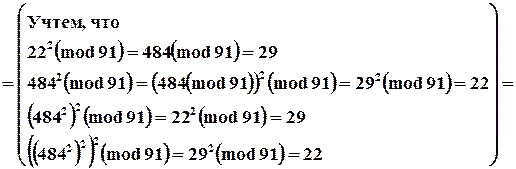
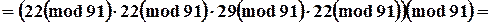
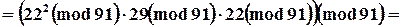
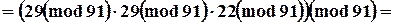
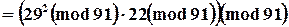
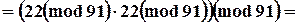
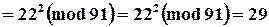
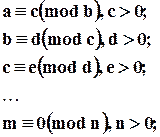Вернемся к алгоритму Эвклида и запишем его алгоритм, с использованием модулярной арифметики. Для описания алгоритма допустим, что
, 
, 
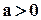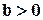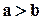, тогда
Найден НОД (a, b) =n
Пример Найти НОД (21, 15)
 |
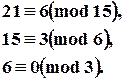т.о. НОД (21, 15)=3.
Проверка согласно свойству 2.1.:
