Пример. Проверим, верно ли сравнение 145º72(mod 16).

Проверим, верно ли сравнение 145º 72(mod 16).

Найдем остатки от деления 145 на 16, 72 на 16.

145 mod 16=1; 72 mod 16=8. 1¹ 8, значит сравнение неверно.

145º 1(mod 16).

72º 8 (mod 16).

Три операции сложение, вычитание и умножение, определенные для Z, могут также быть определены для набора Z_n. Модулярная арифметика аналогична во многом обычной арифметике: она коммутативна, ассоциативна и дистрибутивна. Можно либо сначала приводить по модулю n, а затем выполнять операции, либо сначала выполнять операции, а затем приводить по модулю n.

Приведем свойства сравнений, подобные свойствам отношения равенства.

Пусть есть а º b (mod n) и с º d (mod n), тогда:

Свойство 2. 1 2.. a × c º b × d (mod n)

либо

Свойство 2. 2. (а ± b) (mod n) º [a(mod n) ± b(mod n)] mod n,

Свойство 2. 3. (а × b) (mod n) º [a(mod n) × b(mod n)] mod n,

Свойство 2. 4. [а × (b + с)] (mod n) º {[а × b(mod n)] + [а × c(mod n)]} mod n.

Пример:

(15 + 20) mod 4 º [15 (mod 4) + 20 (mod 4)] mod 4

Можно сокращенно

(15 + 20) mod 4 º 15 (mod 4)+ 20 (mod 4) º 3 (mod 4)+ 0 (mod 4) º (3 + 0) mod 4 º 3 (mod 4)

Т.е. по свойству

а = 3 + k× 4, где k целое число.

Свойство 2. 5. Если

а º b (mod n), то аt º bt (mod n), если t – целое число.

Деление имеет смысл, если

,

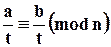когда

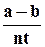– целое число

Пример:

Для числа 18º 4 (mod 14) справедливо умножение, t=2, т.е. 36º 8 (mod 14), но несправедливо деление потому, что

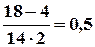– не целое число.

Свойство 2. 6. Из правила умножения вытекает