
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Модулярная арифметика
|
|
Уравнение деления (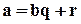 ), рассмотренное в предыдущем разделе, имеет два входа (a и b) и два выхода (q и r). В модулярной арифметике нас интересует только один из выходов – остаток r. Т.о. будем рассматривать целые числа в связи с остатками от деления их на данное целое положительное, называемое модулем.
), рассмотренное в предыдущем разделе, имеет два входа (a и b) и два выхода (q и r). В модулярной арифметике нас интересует только один из выходов – остаток r. Т.о. будем рассматривать целые числа в связи с остатками от деления их на данное целое положительное, называемое модулем.
Определение 2.1. Пусть а, b Î Z, nÎ N. Говорят, что число а сравнимо с b по модулю n, если а и b при делении на n дают одинаковые остатки.
Записывают:
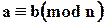 .
.
Сравнимость чисел а и b по модулю n равносильна:
Свойство 2.1. Возможности представить а в форме 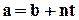 , где t
, где t 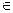 Z.
Z.
Свойство 2.2. Делимости (a–b) на n, т.е. n | (a–b).(имеется ввиду без остатка)
Также запись 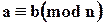 читается так: «a конгруэнтно (тождественно, эквивалентно) числу b по модулю n».
читается так: «a конгруэнтно (тождественно, эквивалентно) числу b по модулю n».
Определение 2.2. Совокупность чисел, сравнимых с a по модулю n называется классом чисел по модулю n (или классом эквивалентности, классом вычетов по модулю n).
Обозначается 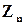 .
.
Из этого определения следует, что все числа одного класса имеют один и тот же остаток r от деления на n и могут быть представлены в виде nt + r при фиксированном r, t 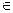 Z.
Z.
Определение 2.3. Любое число класса вычетов называется вычетомпо модулюn по отношению ко всем числам того же класса.
Например, если n = 4, мы имеем множество из четырех элементов [0]4, [1]4, [2]4 и [3]4, таких как это показано ниже:
[0]4 = {…., –12, –8, –4, 0, 4, 8, 12, …}
[1]4 = {…., –11, –7, –3, 1, 5, 9, 13, …}
[2]4 = {…., –10, –6, –2, 2, 6, 10, 14, …}
[3]4 = {...., –9, –5, –1, 3, 7, 11, 15, …}
Целые числа в наборе [0]4 все дают остаток 0 при делении на 4 (сравнимы по модулю 4). Целые числа в наборе [1]4 все дают остаток 1 при делении на 4 (сравнимы по модулю 4), и так далее. В каждом наборе есть один элемент, называемый наименьшим (неотрицательным) вычетом. В наборе [0]4 это элемент 0; в наборе [1]4 – 1, и так далее. Набор, который показывает все наименьшие вычеты: Z4= {0, 1, 2, 3}. Другими словами, набор Zn– набор всех наименьших вычетов по модулю n.
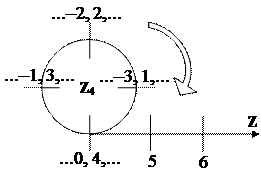
Понять процесс собирания целых чисел в классы сравнимых между собой по модулю n поможет следующая картинка:
На рисунке изображен процесс наматывания цепочки целых чисел на колечко с n делениями, при этом на одно деление автоматически попадают сравнимые между собой числа.
 |
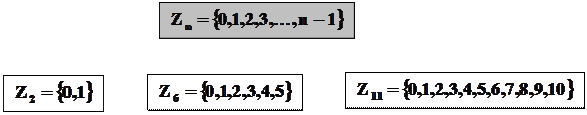 |
Хотя существует только одно множество целых чисел (Z), мы имеем бесконечное число множеств вычетов (
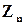 ), но лишь одно для каждого значения n. Рис. показывает множество
), но лишь одно для каждого значения n. Рис. показывает множество 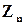 и три множества
и три множества 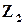 ,
, 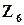 и
и 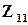 .
.
Рис. Некоторые наборы Zn
Мы пользуемся сравнением по модулю в нашей ежедневной жизни; например, мы применяем часы, чтобы измерить время. Наша система часов использует арифметику по модулю 12. Однако вместо 0 мы берем отсечку 12, так что наша система часов начинается с 0 (или 12) и идет до 11. Поскольку наши сутки длятся 24 часа, мы считаем по кругу два раза и обозначаем первое вращение как утро до полудня, а второе — как вечер после полудня
Если на циферблате часов мы видим 5 часов, то это может означать либо 5 часов утра либо 17 часов вечера. Это арифметика по модулю 12.
Мы привыкли искать остаток от деления по формуле
17 mod 12 = 5
В модулярной арифметике
17 º 5(mod 12).