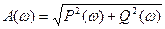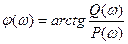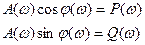Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятие о частотных характеристиках
|
|
Частотные характеристики звеньев и систем отражают зависимость установившихся параметров выходного сигнала для гармонического входного воздействия при изменении частоты от 0 до ¥.
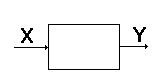
Пусть на вход звена (системы) подается гармонический сигнал 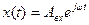 .
.
Если система устойчива, то на выходе установятся колебания с той же частотой, но другой амплитудой и фазой 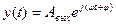 .
.
Вычислим производные от этих сигналов:
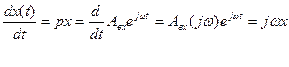

…………………………………………….
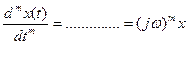
Для выходного сигнала:
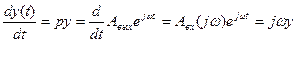
………………………………………..
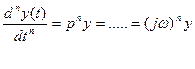
Подставим полученные выражения в исходное выражение (1) и (2):
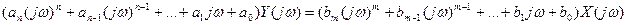
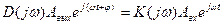
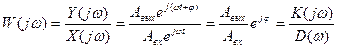
Подобное преобразование уравнения (1) может быть получено также с помощью интегрального преобразования Фурье: 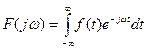 .
.
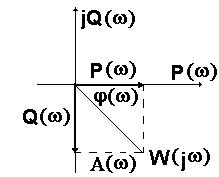
Функция W(jw) называется амплитудно-фазовой характеристикой (АФХ) или комплексно-частотной характеристикой (КЧХ). Для любых значений частоты w функция W(jw) представляет собой вектор на комплексной плоскости, модуль которого равен 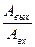 , а аргумент равен углу сдвига фазы выходного сигнала относительно входного.
, а аргумент равен углу сдвига фазы выходного сигнала относительно входного.
При изменении w от -¥ до +¥ вектор будет поворачиваться на комплексной плоскости. Траектория конца вектора (годографа) представляет собой графический образ АФХ.
Выводы:
1. Аналитическое выражение АФХ формально может быть получено из ПФ подстановкой вместо p jw.
2. АФХ может быть построена экспериментально:
a) подаем на вход sin-й сигнал 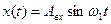 ;
;
b) измеряем на выходе установившееся значение выходного сигнала Авых и j1;
c) вычисляем модуль АФХ 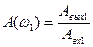 и строим 1-ю точку АФХ
и строим 1-ю точку АФХ
d) повторяя опыт для других частот w1, w2, … строим другие точки.
e) соединяем точки плавной кривой.
Как любая комплексная функция АФХ может быть записана в показательной и алгебраической формах:
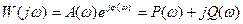
А(w) – АФХ - зависимость отношения амплитуды выходного сигнала к амплитуде входного сигнала от частоты.
j(w) – ФЧХ – фазовая частотная характеристика – зависимость угла сдвига фазы выходного сигнала от частоты.
P(w) – вещественная частотная характеристика ВЧХ.
Q(w) – мнимая частотная характеристика МЧХ.