Радіуси інерції

Момент інерції перерізу щодо якої-небудь осі можна уявити у вигляді добутку площі фігури на квадрат деякої величини, названої радіусом інерції: 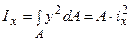, , 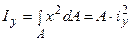відкіля радіуси інерції відповідно щодо осей X і Y: , .

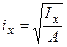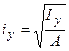Розглянемо приклади обчислення осьових моментів інерції для складених перерізів.

Приклад 5. Обчислимо головні центральні моменти інерції Т - образного перерізу.

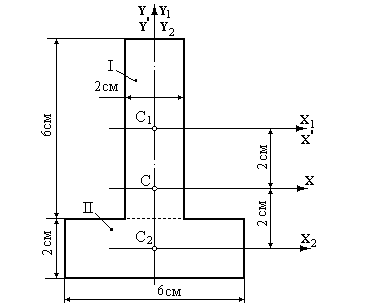
Рис.5.8.

1. Розбиваємо переріз на прості площі, проводимо їхні центральні осі.

2. Вибираємо осі відліку X¢ Y¢, у даному випадку співпадаючими з осями X₁Y₁.

3. Визначаємо координати центрів ваги складових площ: 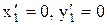; 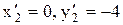см. Так як переріз має одну вісь симетрії Y, то центр ваги перерізу лежить на цій осі. Тому потрібно визначити тільки координату:

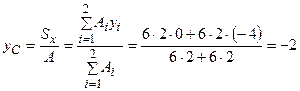см.

Переріз складається з двох рівновеликих площ, тому його центр ваги знаходиться у середині між центрами С₁ і С₂.

4. Визначаємо осьові моменти інерції 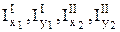щодо власних центральних осей кожної площі, відстан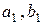і і 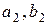між центральними осями перерізу і центральними осями складених площ, та з урахуванням залежності між моментами інерції щодо рівнобіжних осей визначаємо моменти інерції перерізу:

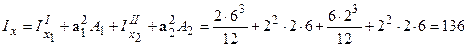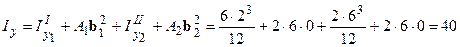см⁴,

см⁴.

Приклад 6. Вирахуємо головні центральні моменти інерції перерізу, показаного на рис. 5.9.

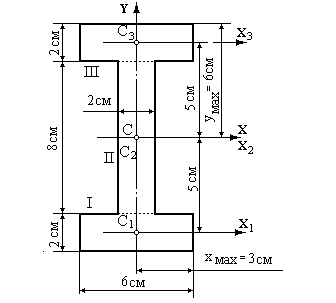
Рис.5.9.

1. Переріз складається з трьох частин, має дві осі симетрії, тому осі симетрії є центральними осями та головними осями інерції.

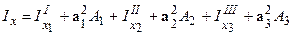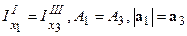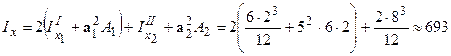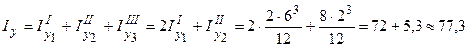2. Осьові моменти інерції перерізу визначаються аналогічно попередньому прикладу: ; , тоді см⁴. см⁴.

3. Осьові моменти опору:

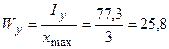см³, см³.

КОНТРОЛЬНІ ПИТАННЯ

1. Як визначається статичний момент фігури через її площу і координати центру тяжіння перетину?

2. Яка розмірність статичного моменту площі?

3. Чому рівний статичний момент площі фігури щодо осі, що проходить через центр тяжіння фігури?

4. По яких формулах визначається центр тяжіння фігури?

5. Що називається осьовим, полярним і відцентровим моментами інерції? Яка їх розмірність?

6. Як зв'язані між собою суми осьових моментів інерції щодо перпендикулярних осей і полярний момент інерції щодо точки перетину цих осей?

7. Які по знаку осьовий, полярний і відцентровий моменти інерції?

8. Напишіть формули, що виражають залежність осьових і відцентрового моментів інерції щодо осей паралельних центральним осям.

9. Чому дорівнюють осьові моменти інерції прямокутного перетину щодо центральних осей, осей паралельних підставі і бічній стороні?

10. Чому дорівнюють центральні осьові моменти інерції круглого і кільцевого перетинів?

11. Як змінюється відцентровий момент інерції при повороті координатних осей на 90 градусів?

12. Які осі називаються головними центральними осями інерції?

13. Чому вісь симетрії перетину завжди є однією з головних осей інерції?

14. Як визначається момент інерції щодо центральної осі складної фігури, якщо її можна розбити на прості фігури, моменти інерції яких легко визначаються по формулах або таблицях?

15. Що називається осьовим моментом опору? Яка його розмірність?

16. Напишіть формули для визначення осьових моментів опору прямокутного, круглого і кільцевого перетинів.