Приклад 2. Обчислення відцентрового моменту інерції.

Визначимо відцентровий момент прямокутника (рис.5.3а). Розіб'ємо на чотири площі, візьмемо елементарні площадки dА у кожнім квадранті, та визначимо елементарний відцентровий момент всього перерізу як суму елементарних відцентрових моментів окремих площ у кожному координатному квадранті:

.

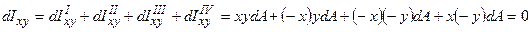Відцентровий момент прямокутника щодо обраних центральних осей дорівнює нулю. Центральні осі X, Y у даному випадку є осями симетрії.

Розглянемо переріз з однією віссю симетрії (рис.5.3б).Поводячись аналогічним образом, маємо: 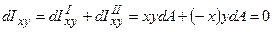. Таким чином, якщо переріз має хоча б одну вісь симетрії, то відцентровий момент інерції щодо центральних осей дорівнює нулю.

Центральні осі X, Y, щодо яких відцентровий момент інерції Ixy дорівнює нулю, називаються головними осями інерції, а осьові моменти інерції Ix і Iy щодо цих осей називаються головними моментами інерції.

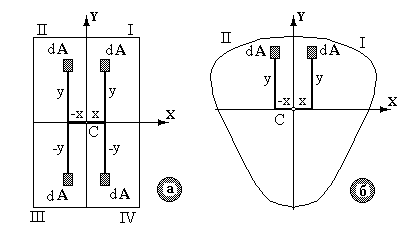
Рис.5.3.

Приклад 3. Визначення осьових моментів інерції для прямокутника.

Осьовий момент інерції щодо центральної осі Х дорівнює 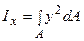. Візьмемо на відстані y елементарну площадку dА – смужку шириною dy. Площа 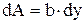, підставимо під інтеграл та проінтегруємо від 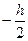до 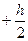. Одержимо: .

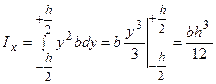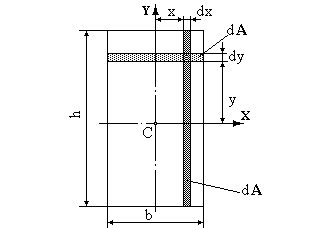
Рис.5.4.

Міркуючи аналогічно, визначимо осьовий момент інерції щодо осі Y, тобто:

.

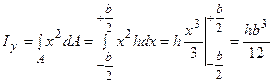Приклад 4. Визначення моментів інерції для круглого перерізу (рис.5.5а).

Визначимо полярний момент інерції 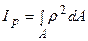. На відстані r виділимо елементарну площадку dА – кільце шириною dr. Очевидно, що 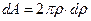. Підставимо значення dА в інтеграл та інтегруємо від 0 до 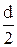. Одержимо: 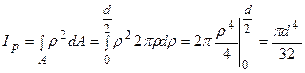. Але полярний момент інерції дорівнює сумі осьових моментів інерції, тобто 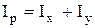. Очевидно, що для круглого перерізу I_x = I_y. Тоді I_p = 2I_x і 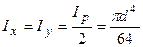. На підставі отриманих формул легко одержати значення моментів інерції для кільцевого перерізу (рис.5.5б). Осьовий момент інерції щодо центральних осей складеного перерізу дорівнює сумі осьових моментів інерції щодо цих осей складених площ, тобто осьовий момент інерції кільцевого перерізу:

,

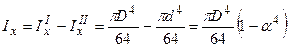тут 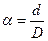. Очевидно і для кільцевого перерізу I_x = I_y. Аналогічно визначимо полярний момент інерції: .

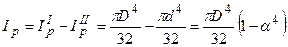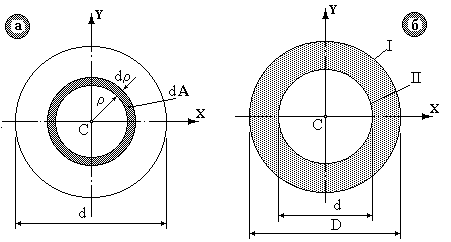
Рис.5.5.