Перевірка правильності побудови епюр.

1.На ділянці з рівномірно розподіленим навантаженням q епюра N(z) лінійна (описується рівнянням прямої лінії, нахиленої до нульової), якщо q=0, то N(z)=const. У нашому випадку на першій і другій ділянках N(z) є лінійною, на третьому - постійна.

2.У перерізах прикладення зосереджених сил на епюрі N(z) спостерігаються стрибки на величини цих сил. У перерізах прикладення сил F₁, F₂ та реакції Н на епюрі маються стрибки на їхні величини відповідно.

Нормальне напруження при центральному розтяганні-стисканні. Розглянемо розтягання прямолінійного стержня довільного поперечного перерізу під дією двох рівних по величині та протилежно спрямованих сил (рис.2.3а). У деякому місці стержня уявно проведемо поперечний переріз, відкинемо одну з частин, дію відкинутої частини замінимо внутрішнім зусиллям N, що з рівняння статичної рівноваги SF_iz = 0 визначиться як N = F (рис.2.3б). Поздовжня сила N є рівнодіючою (результуючою) внутрішніх зусиль довільним образом розподілених по перерізу А, перпендикулярному осі стержня. Отже, поздовжня сила N, спрямована по осі стержня, є нормальною (перпендикулярною) до перерізу. Так як поздовжня сила є результуючою розподілених внутрішніх зусиль (а це нормальне напруження), то і розподілені внутрішні зусилля повинні бути перпендикулярні перерізу. Тобто, при центральному розтяганні (також і при центральному стисканні) у поперечному перерізі виникає тільки нормальне напруження s (рис.2.3.в).

Очевидно, що на елементарну площадку dA діє елементарна поздовжня сила dN = sdA. Відкіля одержуємо рівняння в інтегральному вигляді:

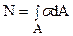. (2.1)

Вирішити це рівняння неможливо, тому що невідома величина та закон розподілу по перерізу напруження s.

Щоб описати закон розподілу напружень s за поперечним перерізом, звернемося до фізичного експерименту. Як показують експерименти, при центральному розтяганні-стисканні однакові подовжні відрізки ас і bd стержня одержують однакові подовження (рис.2.3г): (a ₁ c ₁ – ac) = (b ₁ d ₁ – bd). Лінії на бічній поверхні стержня, що представляють сліди поперечних перерізів, рівнобіжні до деформування, залишаються рівнобіжними й у процесі деформування: ab || a ₁ b ₁ і cd || c ₁ d ₁.

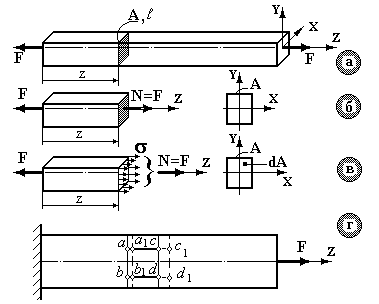
Рис.2.3.

Це дозволяє вважати, що при центральному розтяганні-стисканні виконується гіпотеза плоских перерізів (гіпотеза Бернуллі): переріз плоский та нормальний до осі до деформації залишається плоским та нормальним до осі в процесі деформації, тобто переміщуючись, переріз залишається паралельним (рівнобіжним) самому собі. Якщо представити модель стержня, що складається з окремих подовжніх волокон, то при розтяганні кожне волокно подовжується на одну і ту ж величину. Отже, у кожному подовжньому волокні діє однакове зусилля. Цей висновок дозволяє вважати, що при центральному розтяганні-стисканні нормальне напруження s по поперечному перерізу розподіляється рівномірно, тобто s = сonst.

Тоді з рівняння (2.1) маємо: , відкіля нормальне напруження для всіх точок перерізу при центральному розтяганні-стисканні буде однаковим, і визначиться як:

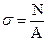. (2.2)

У цьому випадку напруження σ залишаються постійними як по перерізу, так і по довжині (якщо повздовжня сила постійна), тобто по всьому об¢ єму стержня. Такий напружений стан називається однорідним.

Переріз стержня, у якому виникає найбільше нормальне напруження, є небезпечним. У цьому перерізу, як правило, діє і найбільша за абсолютним значенням поздовжня сила N_max.

Максимальні розрахункові нормальні напруження, обчислені за формулоою (2.2), повинні зіставлятися з деякими гранично допустимими напруженнями для матеріалу стержня, що забезпечують його безпечне навантаження. Ці напруження називаються допустимими напруженнями [s]. Сформулюємо умову міцності при центральному розтяганні-стисканні:

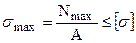. (2.3)

Напруження, що допускається (допустиме напруження), визначається як небезпечне напруження для даного матеріалу s_нб, поділене на коефіцієнт запасу міцності n, тобто 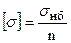: (про небезпечні напруження для матеріалу див. лекцію №4 «Механічні характеристики матеріалів»).

Покажемо основні види розрахунків в опорі матеріалів, які виконуються з використанням умови міцності (2.3) (розрахунки по допустимому напруженню).

1.Перевірочний розрахунок. Основна мета перевірочного розрахунку полягає в порівнянні максимальних розрахункового та допустимого напруження. У цьому розрахунку відомою вважається вся інформація про стержень, що включає три групи даних:

– про зовнішні сили: значення навантажень та координати їхнього прикладення – N_max,

– про геометричні розміри стержня: площа поперечного перерізу – А,

– про механічні властивості матеріалу стержня: допустиме напруження - [s].

За формулою (2.2) обчислюємо s_max і порівнюємо з допустимим [s]. Якщо s_max » [s] – міцність стержня забезпечена (допускається відхилення до 5% у значеннях s_max і [s]). При s_max < [s] стержень є недовантаженим, що приводить до перевитрати матеріалу. У випадку, s_max > [s] – стержень перевантажений, що приводить до необхідності переглянути вихідну розрахункову схему чи вибрати інший матеріал.

2.Проектувальний розрахунок. Основна мета цього розрахунку полягає у визначені безпечних з погляду на міцність розмірів перерізу стержня чи сил, що допускаються. Проектувальний розрахунок проводиться за допомогою умови міцності (2.3).

Підбор площі поперечного перерізу. Відомими вважаються:

– зовнішні сили: значення навантажень і координати точок, де прикладені сили – N_max,

– механічні властивості матеріалу стержня: допустиме напруження - [s].

З умови міцності (2.3) розміри поперечного перерізу обчислюємо за формулою

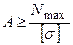. Це значення площі поперечного перерізу стержня А є мінімальною оцінкою для вибору необхідної площі А.

Визначення максимального навантаження. Відомими вважаються:

– геометричні розміри стержня: площа поперечного перерізу – А,

– механічні властивості матеріалу стержня: допустиме напруження - [s].

З умови міцності (2.3) маємо N_max £ [s]× A, відкіля далі визначається навантаження, що допускається.

Переміщення та деформації. Закон Гука. Модуль пружності. Коефіцієнт Пуассона.

Розглянемо розтягнутий силою F стержень довжиною та площею поперечного перерізу А.

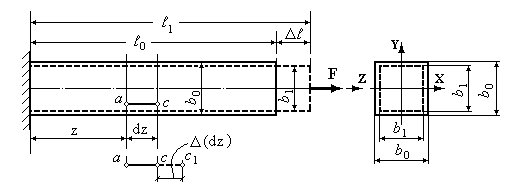
Рис.2.4.

Під дією зовнішнього навантаження, що розтягує, подовжній розмір стержня збільшується до 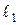. Зміна довжини 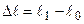називається абсолютним подовженням стержня. Відношення

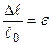(2.4)

називається відносною подовжньою деформацією (або просто подовжньою деформацією). Якщо в стержні виникає неоднорідний напружений стан, деформація в точці а визначається шляхом граничного переходу до нескінченно малого елемента довжиною dz:

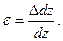(2.5)

При центральному розтяганні-стисканні залежність між навантаженням та подовженням у межах пружних деформацій визначається співвідношенням 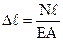, тут Е – модуль пружності (подовжньої пружності) – фізична постійна матеріалу; ЕА – називається жорсткістю стержня при розтяганні. Розділимо обидві частини цього рівняння на 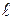і з обліком 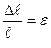, , 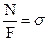отримаємо 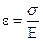або

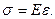(2.6)

Це співвідношення називається законом Гука при центральному розтяганні-стисканні (одновісному напруженому стані). Таким чином, напруження при центральному розтяганні-стисканні обчислюються за формулою 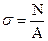. При експериментальному визначенні відносної подовжньої деформації та відомому модулі пружності для матеріалу деталі напруження знаходиться за формулою .

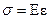Для ділянки стержня нескінченно малої довжини 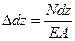. Абсолютне подовження стержня на довжині l визначається за формулою:

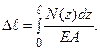(2.7)

Приведемо орієнтовані величини модуля пружності для деяких матеріалів:

- сталь – Е = (2...2, 1)× 10⁵МПа;

-мідь і сплави міді – Е = (1...1, 2)× 10⁵МПа;

- алюміній і сплави алюмінію – Е = (0, 7...0, 72)× 10⁵МПа.

Крім подовжніх деформацій у стержні виникають і поперечні деформації. Різниця 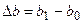(рис. 2.4) називається абсолютною поперечною деформацією. Відношення 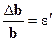називається відносною поперечною деформацією.

Абсолютна величина, що дорівнює відносній поперечній деформації, поділеної на відносну подовжню, називається коефіцієнтом Пуассона 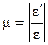. Значення коефіцієнта Пуассона для реальних матеріалів, застосовуваних у машинобудуванні, розташовуються в діапазоні 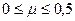(для пробки близько до нуля, для каучуку близько до 0, 5); сталь – m = 0, 25...0, 3; мідь – m = 0, 31...0, 35; алюміній – m = 0, 32...0, 36

Коефіцієнт Пуассона 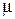також як і модуль подовжньої пружності Е є фізичною константою матеріалу та характеризує його пружні властивості.

Для ізотропних матеріалів Е і 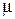в усіх напрямках однакові (сталь, мідь, бетон, каучук, нешаруваті пластмаси), для анізотропних матеріалів Е і 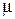у різних напрямках різні (дерево здовж та поперек волокон, шаруваті пластмаси й ін.).

Якщо навантаження, що діє на стержень, є термосиловим, то варто застосувати принцип суперпозиції деформацій, тобто:

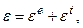(2.8)

де 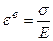– пружна частина, а 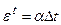– температурна складова деформації, у якій a – температурний коефіцієнт лінійного розширення, тоді

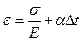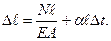або (2.9)

Потенційна енергія пружної деформації. Потенційна енергія деформації, накопичена у пружному тілі, чисельно дорівнює роботі зовнішніх сил, виконаної в процесі деформування пружного тіла, тобто U = W. Розглянемо елемент довжиною dz, навантажений статично (рис.2.5а). У межах нескінченно малого елемента значення поздовжньої сили N(z) у крайніх перерізах елемента dz однакові (рис.2.5.б). Елементарна робота зовнішніх сил чисельно дорівнює площі заштрихованого трикутника, тобто .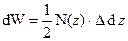

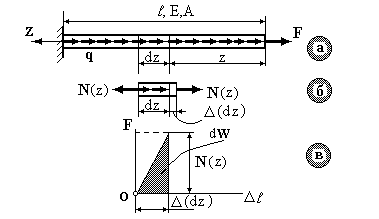
Рис.2.5.

Але 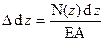, тоді Повна робота є інтеграл по довжині стержня, тобто 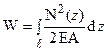. Але , отже:

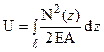. (2.10)