Поняття про напруження. Мірою міцності прийнято вважати напруження, тобто інтенсивність внутрішніх зусиль на одиницю площі.

Класифікація сил. Сили зовнішні та внутрішні.

Сила – це механічна міра взаємодії тіл чи фізичних полів. Сили підрозділяються на зовнішні та внутрішні.

Зовнішні сили. Зовнішні сили підрозділяються на активні і реактивні (реакції зв'язків). Активні навантаження, у свою чергу, підрозділяються на поверхневі - це результат взаємодії двох тіл за допомогою контакту, та об'ємні - результат дії на тіло полів різної природи (сили ваги, інерції, електромагнітні).

За характером навантаження стержнів поверхневі сили розділяються на зосереджені (зосереджена сила F, [H]; зосереджений момент M, [H× м]) і розподілені (рівномірно чи нерівномірно розподілене навантаження q, [H/м] та розподілений момент m, [ ]).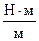

За характером дії зовнішні сили розділяються на статичні та д инамічні. При статичному навантаженні прискореннями часток деформованого тіла можна зневажити, при динамічному навантаженні виникають значні прискорення часток деформованого тіла і, як наслідок, з'являються значні сили інерції, якими зневажати не можна.

Внутрішні сили (зусилля) виникають між суміжними частинами тіла в результаті їхньої взаємодії при його навантаженні. Для визначення внутрішніх зусиль в опорі матеріалів використовується метод перерізів, що складається в послідовному виконанні наступних операцій (див. рис.1.2).

Будемо вважати, що стержень навантажений статично урівноваженою системою зовнішніх сил, яка включає активні та реактивні.

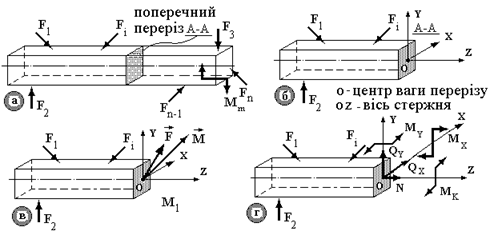
Рис.1.2.

1.Внутрішні зусилля виявляються, якщо у деякому поперечному перерізі А-А уявно розділимо стержень площиною, що збігається з перерізом А-А (рис. 1.2а). Внутрішні зусилля визначають взаємодіі між частками стержня, розташованого з обох сторін уявного перерізу А-А, причому за принципом дії та протидії ліворуч і праворуч від перерізу А-А є взаємними: рівними по величині та протилежними по напрямку, і кожна з частин знаходиться в рівновазі.

2.Далі відкидаємо одну з частин (рис. 1.2б).

3.Дію відкинутої частини, що залишилася, заміняємо внутрішніми зусиллями, які визначаються за принципом дії та протидії. Вони взаємні за принципом дії та протидії. Закон неперервного розподілу внутрішніх зусиль у перерізі А-А невідомий. Внутрішні зусилля у перерізі розподіляються складним образом і довільно орієнтованими в декартовій системі координатних осей X, Y, Z, початок якої міститься в центрі ваги перерізу А-А.

4.Відповідно до теореми про приведення сил до довільної точки простору в загальному випадку внутрішні зусилля приводяться в центр ваги перерізу до головного вектора 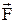і головного моменту 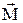(рис.1.2в), приведеного до центру ваги перерізу. Розкладаючи головні вектори 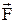і 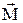по трьом напрямкам X, Y, Z, одержуємо, що результат дії внутрішніх зусиль приводиться до поперечних сил Q_x і Q_y, поздовжньої сили N, згинальним моментам M_x і M_y і крутильному моменту Мк (рис.1.2г). Складов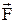і і 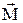мають загальну назву внутрішніх силових факторів.

Для частини, що залишилась і знаходиться під дією зовнішніх і внутрішніх сил, складаємо рівняння рівноваги, з яких відповідно знаходимо внутрішні силові фактори Qx, Qy, N, Mx, My, Мк в поперечному перерізі:

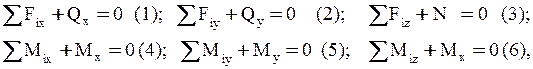
де SF_{ix, y, z} і SM_{ix, y, z} відповідно суми проекцій усіх зовнішніх сил на осі X, Y, Z та суми моментів усіх зовнішніх сил щодо осей X, Y, Z. Внутрішні силові фактори Q_x, Q_y, N, M_x, M_y, M_к є інтегральними рівнодіючими силами і моментами внутрішніх зусиль, що насправді складним образом розподіляються по поперечному перерізу.

По виникаючим у перерізі внутрішнім силовим факторам проводиться класифікація типів навантаження стержня (видів деформування). Так, якщо із шести внутрішніх силових факторів у перерізі відмінною від нуля є тільки поздовжня сила N ¹ 0, то в стержні реалізується розтягання-стискання; при M_к ¹ 0 - кручення і т.д.

Поняття про напруження. Мірою міцності прийнято вважати напруження, тобто інтенсивність внутрішніх зусиль на одиницю площі.

У перерізі А-А в околиці точки К виділимо нескінчено малу площу (елементарну площадку) DА, на яку діє елементарна сила 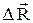- рівнодіюча внутрішніх зусиль на цій частині перерізу (рис.1.3).

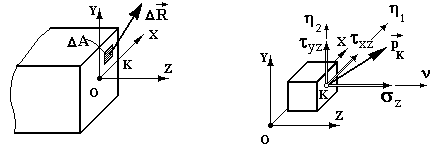
Рис. 1.3. Рис. 1.4.

Середнє напруження в точці К вводиться як відношення елементарної сили 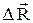до величини нескінченно малої площадки Δ Α в околиці точки К: 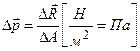. Механічні напруження, як правило, є великими величинами та розраховуються в МПа (1МПа = 10⁶Па).

Повне напруження в точці К одержуємо граничним переходом при стягуванні площадки DА до нуля: 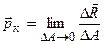. Розкладемо повне напруження в точці К на складові: по нормалі n і по дотичним h ₁, h ₂ до площадки (рис.1.4). Нормальна складова s _z (чи просто s) називається нормальним напруженням, дотичні складові t _xz, t _yz – дотичними напруженнями.

Нормальне напруження s викликає деформацію розтягання чи стискання. Напруження вважається позитивним (додатним), якщо викликає деформацію розтягання і негативним (від’ємним), якщо - стискання. Надалі індекс «z» часто буде опускатися, що зв'язано з традиційним розглядом схеми стержня в опорі матеріалів.

Дотичне напруження викликає деформацію зсуву (зрізу) і вважається позитивним, якщо обертає розглянуту область щодо точки усередині цієї області за годинниковою стрілкою, та навпаки.

Якщо через точку тіла провести іншу площину перетину, то нормальне і дотичне напруження змінюються. Сукупність нормальних і дотичних напружень на безлічі площин, що проходять через дану точку тіла, утворюють напружений стан у цій точці тіла.

Поняття про переміщення та деформації. Під дією зовнішніх сил тверде тіло змінює свої розміри та форму (деформується). Вектор, що має початок у точці недеформованого тіла, а кінець у тій же точці деформованого тіла, називається повним лінійним переміщенням точки. Проекції повного переміщення на осі X, Y, Z позначаються u, v, w відповідно. Крім лінійного переміщення, можна ввести поняття кутового переміщення, як кута повороту між положеннями фіксованого елемента тіла в недеформованому і деформованому станах.

Для характеристики інтенсивності зміни форми та розмірів вводиться її міра – лінійна та кутова деформації. До навантаження тіла зафіксуємо на поверхні тіла прямий кут Ð ВАС зі сторонами рівними s(рис.1.5).

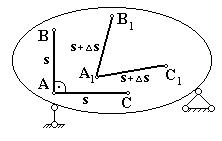
Рис. 1.5.

В результаті деформування тіла ці відстані змінилися на малі величини Ds. Відношення збільшення довжини відрізка АВ до його початкової довжини називається середньою деформацією на відрізку s: . Зменшуючи відрізок АВ (наближаючи точку А до точки В) внаслідок одержимо величину лінійної деформації (іноді просто деформації) у точці А по напрямку АВ: .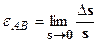

Кутова деформація (деформація зсуву, кут зсуву) вводиться як ступінь зміни початкового прямого кута при деформуванні тіла. Кутова деформація в точці А в площині ВАС: 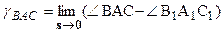.