Нормальні та дотичні напруження на похилих площадках.

Розглянемо стержень з поперечним перерізом А₀, навантажений силою F. У нормальному (перпендикулярному осі Z) перерізі виникають нормальні напруження 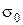, що визначаються як 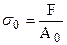. А які напруження виникають на площадці A_a, нахиленої до осі стержня під кутом a? Положення площадки A_a визначається положенням її нормалі n_a (рис.2.6а). Так як зовнішнє навантаження збігається з віссю стержня, то і на будь-якій похилій площадці внутрішні зусилля (напруження) збігаються з віссю стержня, у даному випадку це буде повне напруження p_a, яке визначається за формулою 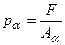(рис.2.6б). Площа похилого перерізу 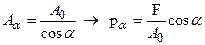. Але 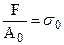, тоді повне напруження 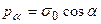. Так як 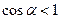, то завжди 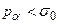. Розкладемо повне напруження p_a на дві складові: нормальну та дотичну до площадки A_a (рис.2.6в). Одержимо нормальне s_a і дотичне t_a напруження на похилій площадці. Нормальне напруження на похилій площадці з нормаллю n_a:

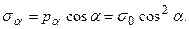(2.11)

Рис.2.6.

Дотичне напруження на похилій площадці з нормаллю n_a:

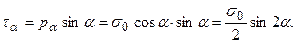(2.12)

Нормальне напруження s_a позитивне (викликає деформацію розтягання), дотичне t_a теж позитивне, тому що обертає розглянуту область щодо точки у середині цієї області за годинниковою стрілкою. Визначимо напруження на взаємно перпендикулярній площадці A_b, нахиленої до осі стержня під кутом b, що дорівнює 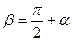(рис.2.6г). Якщо 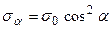, то, мабуть, і 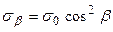. Підставивши 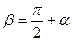, , 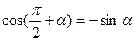одержимо:

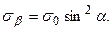(2.13)

Аналогічно 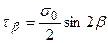. Підставивши 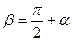, , 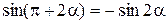одержимо:

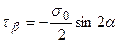. (2.14)

Нормальне напруження 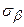також позитивне, а дотичне 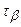- негативне (обертає розглянуту область щодо точки у середині цієї області проти годинникової стрілки). Склавши вирази (2.11) і (2.13), одержимо 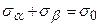, сума нормальних напружень на двох взаємно перпендикулярних площадках постійна. Порівнюючи (2.10) і (2.14), маємо 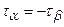. Ця рівність відбиває закон парності дотичних напружень: дотичні напруження на двох взаємно перпендикулярних площадках рівні по величині та протилежні по напрямку. Якщо відоме дотичне напруження на одній площадці, то на інших перпендикулярних площадках дотичні напруження визначаються за вищевказаним законом парності (рис.2.6г).

КОНТРОЛЬНІ ПИТАННЯ

1. В чому полягає суть гіпотези плоских перетинів?

2. Що називається повним або абсолютним подовженням?

3. Що називається відносним подовженням (відносною деформацією). Яка його розмірність?

4. Сформулюйте закон Гука; як він виражається математично?

5. Що характеризує модуль поздовжньої пружності?

6. Чи всі матеріали підкоряються закону Гука?

7. Що називається жорсткістю стрижня при розтяганні-стисканні?

8. Що таке коефіцієнт Пуассона?

9. Які характерні крапки має діаграма розтягання-стискання для маловуглецевої сталі?

10. Що називається межею пропорційності, межею пружності, межею текучості, тимчасовим опором (межею міцності)?

11. Як може бути визначена величина модуля подовжньої пружності 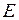з діаграмою розтягання для матеріалу?

Лекція№3. Статично невизначені системи (СНС) при розтяганні-стисканні.

Статично невизначеною називається кінематично незмінна система, у якої число невідомих зусиль, включаючи реакції опор та внутрішні сили, більше числа рівнянь статичної рівноваги, які можна скласти для даної задачі. Різниця між кількістю невідомих зусиль та кількістю незалежних рівнянь статичної рівноваги називається ступенем статичної невизначеності системи. Це число показує, скільки додаткових рівнянь у геометричному аналізі процесу деформування необхідно скласти, щоб можна було вирішити задачу. При рішенні таких систем розглядаємо три сторони задачі. План рішення полягає в наступному.

1. Статична сторона задачі (ССЗ). Визначаємо напрямок реакцій зв'язків, зусиль у стержнях, складаємо рівняння рівноваги, визначаємо ступінь статичної невизначеності задачі.

2. Геометрична сторона задачі (ГСЗ). Установлюємо зв'язок між деформаціями окремих елементів конструкції, виходячи з умови спільності переміщень. Отримані рівняння називаються рівняннями спільності переміщень.

3. Фізична сторона задачі (ФСЗ). У рівняннях спільності переміщень для окремих елементів їхні переміщення виражаємо на підставі закону Гука через діючі в них невідомі зусилля.

4. Аналіз (синтез). Вирішуємо отриману систему рівнянь щодо невідомих зусиль.

Розглянемо рішення СНС на прикладах.

Приклад 1. Стержень довжиною (a+b) і площею поперечного перерізу А навантажений силою F. Модуль пружності матеріалу Е. Визначити опорні реакції та побудувати епюру поздовжніх сил.

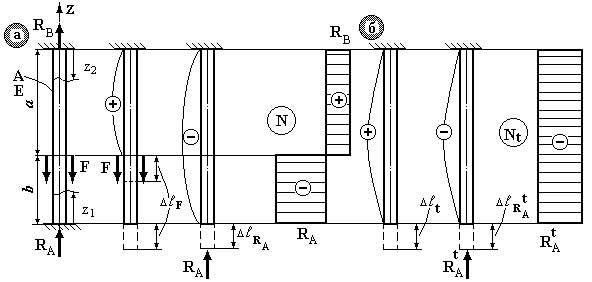
Рис.3.1.

1. ССЗ. Показуємо опорні реакції R_A і R_B. Записуємо єдину умову рівноваги, яку можна скласти для даної задачі:

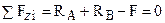. (3.1)

2. ГСЗ. Так як опори жорсткі, то повне подовження стержня дорівнює нулю, тобто 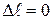. Один з підходів реалізації цієї умови такий. Відкидаємо одну з опор (допустимо нижню) та послідовно прикладаємо зовнішні сили і невідому реакцію у відкинутій опорі. Повне подовження стержня визначаємо як суму подовжень від зовнішнього навантаження (у даному випадку 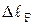) від реакції :

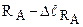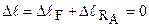. (3.2)

3. ФСЗ. Подовження від зовнішнього зусилля у розглянутому випадку складає: 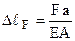, укорочення від реакції: 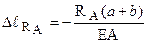, тому повна деформація стержня виявляється рівною:

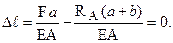(3.3)

4. Аналіз. З рівняння (3.3) одержуємо 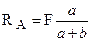, а з рівняння (3.1) маємо: 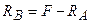. Розбиваємо стержень на дві ділянки та записуємо значення поздовжньої сили на кожній ділянці:

1^а ділянка: 0 £ z₁£ b: 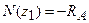; 2^а ділянка: 0 £ z₂£ a: .

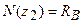Далі будуємо епюру поздовжніх сил.

Особливий інтерес викликають задачі розрахунків СНС при термосиловому навантаженні. Відзначимо, що в статично визначних стержневих конструкціях при нагріванні-охолодженні напруження не виникають, якщо матеріал однорідний.