
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
У статично невизначених стержнях і стержневих системах навіть невеликі перепади температур приводять до появи значних величин напружень.
|
|
Доповнимо вище розглянутий приклад розрахунком температурних напружень. Будемо вважати, що стержень нагрітий на 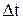 °С. Реакції
°С. Реакції 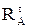 і
і 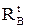 , що виникають у защемленнях, рівні між собою та спрямовані в протилежні сторони. Повне подовження стержня складеться з суми подовжень: вільного температурного розширення стержня
, що виникають у защемленнях, рівні між собою та спрямовані в протилежні сторони. Повне подовження стержня складеться з суми подовжень: вільного температурного розширення стержня 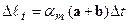 (aТ - коефіцієнт лінійного температурного розширення) та подовження від реакції
(aТ - коефіцієнт лінійного температурного розширення) та подовження від реакції 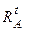 (див. рис.3.1), тобто
(див. рис.3.1), тобто
 , або
, або 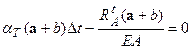 .
.
Тоді одержуємо 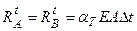 - і значення поздовжньої сили на всіх ділянках стержня постійно:
- і значення поздовжньої сили на всіх ділянках стержня постійно:
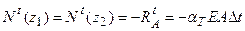 ,
,
що говорить про викликане нагріванням (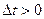 ) стискання стержня.
) стискання стержня.
У цьому випадку температурні напруження у перерізі стержня 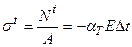 , і, як видно, не залежать від площі поперечного перерізу.
, і, як видно, не залежать від площі поперечного перерізу.
Аналогічно розглядається задача визначення і монтажних напружень, викликаних наявністю монтажного зазору d (перевищення на величину d довжини стержня в порівнянні з відстанню між опорами).
Замінивши температурне Δ ℓ t  подовження на величину зазору δ та виконавши аналогічні перетворення, маємо:
подовження на величину зазору δ та виконавши аналогічні перетворення, маємо: 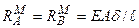 , значення поздовжньої сили
, значення поздовжньої сили 
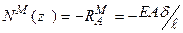 , монтажних напружень
, монтажних напружень 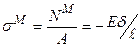 .
.
Приклад 2. Стержнева система (рис.3.2) складається з абсолютно твердого стержня AD, що шарнірно закріплений у точці А та підтримується стержнями 1 і 2 (довжини 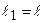 та
та 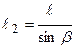 , площі поперечних перерізів А1, А2, модулі пружності матеріалу стержнів Е1, Е2), навантажена зовнішньою зосередженою силою F. Виразити поздовжні сили в стержнях N1 і N2, через зовнішнє навантаження F.
, площі поперечних перерізів А1, А2, модулі пружності матеріалу стержнів Е1, Е2), навантажена зовнішньою зосередженою силою F. Виразити поздовжні сили в стержнях N1 і N2, через зовнішнє навантаження F.
1.ССЗ. Застосовуємо метод перерізів до стержнів, у яких виникають поздовжні сили N1 і N2, прикладаємо реакції опори RA і НА. Відсічена схема показана на рис.3.3а. Складаємо рівняння статичної рівноваги (для плоскої системи сил):
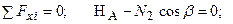 (3.4)
(3.4)
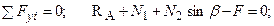 (3.5)
(3.5)
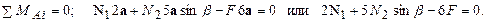 (3.6)
(3.6)
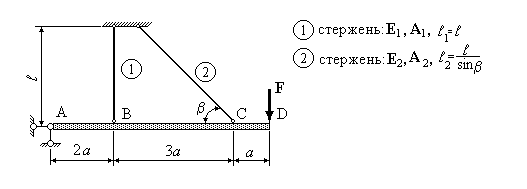
Рис.3.2.
2.ГСЗ. Під дією зовнішнього навантаження стержні 1 і 2 деформуються, а брус AD займе нове положення AD¢ (рис.3.3б). Відповідно точки В и С займуть положення В¢ і С¢. Покажемо деформації стержнів. Подовження стержня 1 - 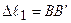 . Щоб знайти деформацію похилого стержня 2, потрібно з нового положення точки С¢ опустити перпендикуляр на початкове положення стержня 2. Різниця кінцевої та початкової довжини складе подовження стержня, тобто
. Щоб знайти деформацію похилого стержня 2, потрібно з нового положення точки С¢ опустити перпендикуляр на початкове положення стержня 2. Різниця кінцевої та початкової довжини складе подовження стержня, тобто 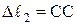 ¢ ¢.
¢ ¢.
Через малість деформацій стержнів у порівнянні з розмірами стержневої системи переміщення точок В, С, D при повороті абсолютно твердого бруса вважаємо таким, що відбуваються не по дузі, а у перпендикулярному напрямку (по нормалі) до початкового положення бруса.
З подоби трикутників АВВ¢ і АСС¢ маємо:
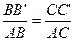 . З огляду на те, що АВ=2 а, АС=5 а, ВВ¢ =
. З огляду на те, що АВ=2 а, АС=5 а, ВВ¢ = 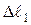 ,
, 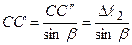 , одержуємо:
, одержуємо:
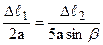 .
.
Рівняння спільності переміщень одержуємо у вигляді:
 . (3.7)
. (3.7)
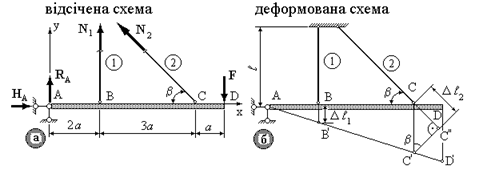
Рис.3.3.
3.ФСЗ. З огляду на те, що подовження стержня визначається рівнянням 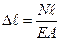 Þ
Þ 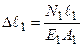 ,
, 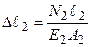 , умова (3.7) прийме вигляд:
, умова (3.7) прийме вигляд: 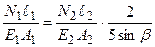 . Після перетворень одержимо:
. Після перетворень одержимо:
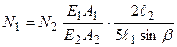 . (3.8)
. (3.8)
4.Аналіз. Вирішуючи спільно рівняння (3.8) і (3.6), одержимо:
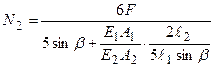 . (3.9)
. (3.9)
Поздовжня сила N1 визначається рівнянням (3.8).
Відзначимо особливості стержневих статично невизначених систем. Переваги цих систем полягають у автоматичному перерозподілі зусиль між стержнями. До недоліків відноситься їх висока чутливість до неточності виготовлення та зміни температури.
Приклад 3. Монтажні напруження. Розглянемо визначення монтажних напружень на прикладі вище проаналізованої стержневої системи. Допустимо, другий стержень виготовлений довшим на величину d2> 0. Після зборки системи брус займе проміжне положення AD¢.
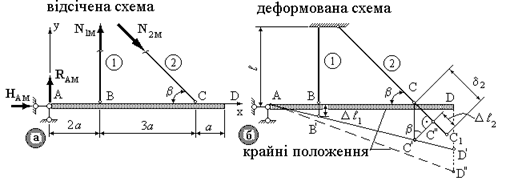
Рис.3.4.
З аналізу деформованої схеми (рис3.4б) випливає, що перший стержень подовжується, у ньому виникає розтягуюче зусилля N1М, другий коротшає - стискаюче зусилля N2М, у шарнірно нерухомій опорі виникають реакції RAМ і HAМ.
ССЗ.
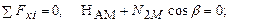 (3.9)
(3.9)
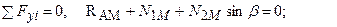 (3.10)
(3.10)
 (3.11)
(3.11)
2.ГСЗ. З подоби трикутників АВВ¢ і АСС¢ маємо: 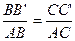 . З огляду на те, що
. З огляду на те, що 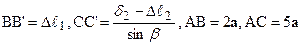 , одержуємо:
, одержуємо: 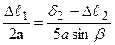 .
.
Тоді рівняння спільності переміщень прийме вигляд:
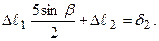 (3.12)
(3.12)
3.ФСЗ. З огляду на закон Гука у формі: 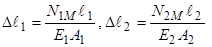 та, підставляючи ці рівняння в умову (3.12), одержуємо:
та, підставляючи ці рівняння в умову (3.12), одержуємо: 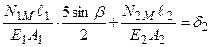 , чи:
, чи:
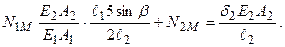 (3.13)
(3.13)
4.Аналіз. Вирішуючи спільно рівняння (3.13) і (3.11), маємо:
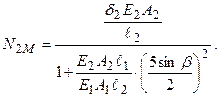 (3.14)
(3.14)
Поздовжня сила N1М визначається рівнянням (3.11). Монтажні напруження обчислюємо за формулами 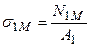 ,
, 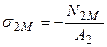 .
.