Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Залежність моментів інерції щодо двох рівнобіжних осей, одна з яких центральна.
|
|
Дано: переріз площею A; відоме положення центральних осей X, Y; відомі осьові Ix і Iy та відцентровий моменти інерції Ixy. Визначити моменти інерції Ix1, Iy1, Ix1y1 щодо осей X1 і Y1, рівнобіжних центральним осям, якщо відомі відстані a і b між осями.
Виділимо елементарну площадку dА та визначимо її координати в системі координат X1Y1: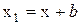 
; 
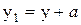. Осьовий момент інерції щодо осі X1 запишеться як: 
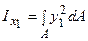. Підставимо значення х1 і y1 та інтегруємо, одержимо: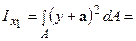 
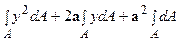. Перший інтеграл являє собою осьовий момент інерції щодо центральної осі X: 
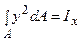; другий – статичний момент площі щодо центральної осі тотожно дорівнює нулю: 
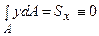; третій 
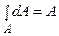– площа перерізу. Таким чином: 
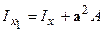. Аналогічно визначимо осьовий момент інерції щодо осі Y1:
, (
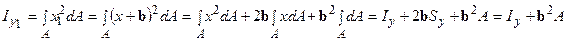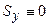, тому що вісь Y – центральна). Таким чином, осьовий момент інерції щодо осі, рівнобіжної центральній осі, дорівнює осьовому моменту інерції щодо центральної осі плюс добуток площі на квадрат відстані між осями.
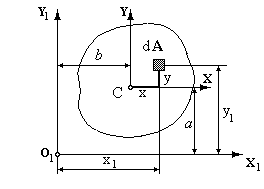
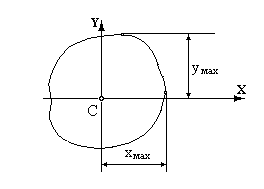
Рис.5.6. Рис.5.7.
Аналогічно визначимо відцентровий момент інерції:
.
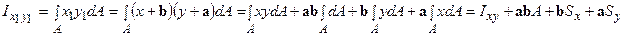З обліком того, що Sx і Sy º 0, маємо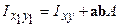 
. Відцентровий момент інерції щодо осей, рівнобіжних центральним осям, дорівнює відцентровому моменту інерції щодо центральних осей плюс добуток площі на відстані між осями, які потрібно брати з відповідними знаками.
Моменти опору. Розглянемо переріз площею A. Х, Y – головні осі перерізу, Ix, Iy – головні осьові моменти інерції. Відношення осьового моменту інерції щодо осі до відстані до найбільш віддаленої точки перерізу від цієї осі називається осьовим моментом опору, тобто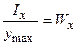 
, 
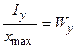[м3].
Практичне значення мають моменти опору щодо головних центральних осей для симетричних фігур, що звичайно називають просто моментами опору.
1. Для прямокутника (рис.5.4):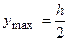 
, 
, 
, 
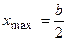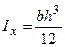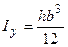, тоді 
, 
.
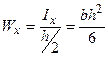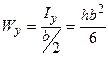2. Для круглого перерізу (рис.5.5а):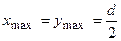 
, 
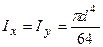, тоді 
.
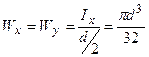3. Для кільцевого перерізу (рис.5.5б):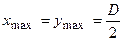 
, 
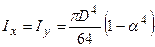, тоді
.
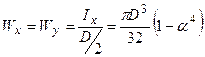Полярним моментом опору називається відношення полярного моменту інерції до відстані від полюса до найбільш віддаленої точки: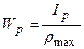 
, [см3, м3]. Для круглого перерізу: 
, 
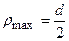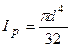, тоді 
. Для кільцевого перерізу: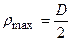 
, 
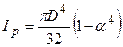, тоді 
.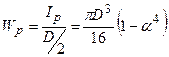