
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кинематический анализ.
|
|
Кинематический синтез кривошипно-ползунного механизма.
Первоочередной задачей проектирования кривошипно-ползунного механизма является его синтез, т. е. определение размеров звеньев по некоторым первоначально заданным параметрам.
· Ход ползуна S =0.125 м.
· Эксцентриситет e =0, т.е. опоры механизма находятся на одном уровне.
· Максимальный угол давления между шатуном и кривошипом qmax =
Отношение длины кривошипа к длине шатуна l = l1/l2 находим из DAOB:
l=l1/l2=sin qmax, (2)
l=0.24.
Длину кривошипа l 1 определяем из рассмотрения двух крайних положений механизма, определяющих ход ползуна S:
S=OB1-OB2=(l1+l2)-(l2-l1)=2l1, (3)
Откуда
l1=S/2, (4)
l1=0.125/2=0.0625 м.
Длина шатуна:
l2=l1/l, (5)
l2=0.0635/0.24=0.264 м.
Расстояние от точки А до центра масс S 2 шатуна
l3=0.35× l2, (6)
l3=0.32× 0.26=0.092 м.
Угловая скорость кривошипа w 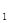 :
:
w1=210
План положений.
План положений - это графическое изображение механизма в n последовательных положениях в пределах одного цикла.
План положений строим в двенадцати положениях, равностоящих по углу поворота кривошипа. Причем все положения нумеруем в направлении вращения кривошипа w 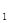 . Положения остальных звеньев находим путем засечек. За нулевое (начальное) положение принимаем крайнее положение, при котором ползун наиболее удален от кривошипного вала (начало работы хода). Начальное положение кривошипа задается углом j 0, отсчитанным от положительного направления горизонтальной оси кривошипного вала против часовой стрелки. Кривая, последовательно соединяющая центры S
. Положения остальных звеньев находим путем засечек. За нулевое (начальное) положение принимаем крайнее положение, при котором ползун наиболее удален от кривошипного вала (начало работы хода). Начальное положение кривошипа задается углом j 0, отсчитанным от положительного направления горизонтальной оси кривошипного вала против часовой стрелки. Кривая, последовательно соединяющая центры S 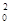 , S
, S 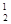 , S
, S 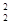 …S
…S 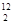 масс шатуна в различных его положениях, будет траекторией точки S 2.
масс шатуна в различных его положениях, будет траекторией точки S 2.
Выбираем масштабный коэффициент длин ml:
m 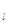 =l2/OA, (7)
=l2/OA, (7)
где l 2 - действительная длина кривошипа, м;
OA- изображающий её отрезок на плане положений, мм.
ml=0.26/300 =0.000866 м/мм.
Отрезок AB, изображающий длину шатуна l 2на плане положений, будет:
AB=l2/ml, (8)
AB=0.26/0.000866= 300 мм.
Расстояние от точки А до центра масс S 2 шатуна на плане положений:
AS2=l3/ml, (9)
AS2=0.085/0.000866 =98.15 мм.
Вычерчиваем индикаторную диаграмму с таким же масштабом перемещения ms =0.000866м/мм, в каком представлен план положений механизма, для которой выбираем масштабный коэффициент давления:
mp=Pmax/Lp, (10)
где Pmax -максимальное давление в поршне, МПа.
Lp -изображающий его отрезок на индикаторной диаграмме, мм.
mp=4/192=0.02083 МПа/мм.
Кинематическую схему механизма вычерчиваем на листе 1 в указанном масштабном коэффициенте ml =0.000866м/мм.
План скоростей и ускорений.
План скоростей – это графическое изображение в виде пучка лучей абсолютных скоростей и точек звеньев и отрезков, соединяющих концы лучей, представляющих собой отношение скорости точек в данном положении механизма.
Определение плана ускорений аналогично определению плана скоростей.
Планы скоростей и ускорений будем рассматривать для десятого положения.
План скоростей.
Скорость точки А находим по формуле:
VA=w1× l1, (11)
где w 1 – угловая скорость кривошипа, с-1.
l 1 – длина кривошипа, м.
VA=210× 0.063=13.23 м/с
Выбираем масштабный коэффициент плана скоростей mV:
mV=VA/Pa, (12)
где VA -скорость точки A, м/с;
Pa -изображающий ее отрезок на плане скоростей, мм.
mV=13.23/100=0.1323
Из полюса P в направлении вращения кривошипа перпендикулярно к OA откладываем отрезок Pa, изображающий вектор скорости точки A, длиной _мм.
Определяем скорость точки В:
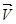 B=
B= 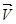 A+
A+ 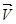 BA, (13)
BA, (13)
где 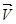 BA - вектор скорости точки B в ее вращательном движении относительно точки A, перпендикулярно к оси звена AB.
BA - вектор скорости точки B в ее вращательном движении относительно точки A, перпендикулярно к оси звена AB.
Из точки а на плане скоростей перпендикулярно оси звена AB проводим прямую до пересечения с линией действия скорости точки B, в результате чего получаем отрезок Pb =96.97мм, изображающий вектор скорости точки B и отрезок ab =53мм, изображающий вектор скорости звена AB.
Тогда
VB=Pb× mV, (14)
VB=96.97× 0.1323=12.83 м/c;
VBA=ab× mV, (15)
VBA=53× 0.1323=7.01 м/с.
Скорость точки S 2 находим из условия подобия:
as2/ab=AS2/AB, (16)
Откуда
as2=(AS2/AB)× ab, (17)
as2=(105/300)× 53=18.5 мм.
Соединив точку S 2 с полюсом P, найдем отрезок, изображающий вектор скорости точки S 2, т.е. Ps 2=95мм.
Тогда
VS2=Ps2× mV, (18)
VS2=95× 0.1323=12.6 м/с.
Если из произвольной точки отложить вектор VS 2 для всех двенадцати положений и соединить их конечные точки плавной кривой, то получим годограф скорости точки S 2.
По результатам расчета программы ТММ1 строим годограф скорости точки S 2.
Угловую скорость шатуна AB определяем по формуле:
w2=VBA/l2, (19)
w2=7.01/0.26=26.96 c-1.
План ускорений.
Находим нормальное ускорение точки A:
aA=w 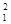 × l1, (20)
× l1, (20)
aA=2102× 0.063=2778.3 м/с2.
Выбираем масштабный коэффициент плана ускорений ma:
ma=aA/Pa, (21)
где aA – нормальное ускорение точки A, м/с2;
Pa – изображающий ее отрезок на плане ускорений, мм.
ma=2778.3/100=27.783 (м/с2)/мм.
Из полюса P откладываем отрезок Pa, изображающий вектор нормального ускорения точки A кривошипа, который направлен к центру вращения кривошипа.
Определяем ускорение точки B:
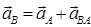 , (22)
, (22)
где 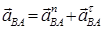 - вектор ускорения точки B в ее вращательном движении относительно точки A.
- вектор ускорения точки B в ее вращательном движении относительно точки A.
Определяем ускорение a 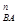 :
:
a 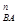 =V
=V 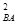 × l2, (23)
× l2, (23)
a 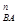 =26.9612× 0.26=189 м/c2.
=26.9612× 0.26=189 м/c2.
Из точки a на плане ускорений проводим прямую, параллельную оси звена AB и откладываем на ней параллельно отрезку AB в направлении от точки B к точке A отрезок an, представляющий собой ускорение a 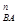 в масштабе ma.
в масштабе ma.
an=a 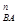 /ma, (24)
/ma, (24)
an=189/27.783=6.80 (м/c2)/мм.
Из точки n проводим прямую перпендикулярную оси звена AB до пересечения с линией действия ускорения точки B, в результате чего получаем отрезок nb =86мм, изображающий вектор касательного ускорения звена AB и отрезок Pb= 40мм, изображающий вектор скорости точки B.
Тогда
a  =nb× ma, (25)
=nb× ma, (25)
a  =86× 27.783=2389.3 м/с2;
=86× 27.783=2389.3 м/с2;
aB= Pb× ma, (26)
aB=40× 27.783=1110.78 м/c2.
Соединив точки a и b, получим отрезок ab= 86мм, изображающий вектор ускорения звена AB.
Тогда
aBA=ab× ma, (27)
aBA=86× 27.783=2389.3 м/с2.
Ускорение точки S 2 находим из условия подобия:
as2/ab=AS2/AB, (28)
Откуда
as2=(AS2/AB)× ab, (29)
as2=(105/300)× 86=30.1 мм.
Соединив точку s 2 с полюсом P, найдем отрезок, изображающий вектор скорости точки S 2, т.е. Ps 2=74мм.
Тогда
aS2=Ps2× ma, (30)
aS2=74× 27.783=2056.1 м/с2.
Если из произвольной точки отложить вектор aS 2 для всех двенадцати положений и соединить их конечные точки плавной кривой, то получим годограф ускорения точки S 2.
По результатам расчета программы ТММ1 строим годограф ускорения точки S 2.
Угловое ускорение шатуна AB определяем по формуле:
e2= a  /l2, (31)
/l2, (31)
e2=2389.3/0.26=9200.2 c-2.