Числовые ряды с положительными членами. Интегральный признак.

Рассмотрим числовой ряд ,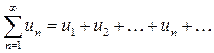

где 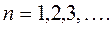для такого ряда 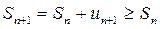. Значит, последовательность частичных сумм возрастает.

Из теоремы о пределе монотонной последовательности можно сформулировать условие сходимости ряда с положительными членами.

Ряд с положительными членами всегда имеет сумму и эта сумма конечна, а ряд будет сходящимся, если частичные суммы ряда ограничены сверху, и бесконечна, а ряд расходящимся в противном случае.

Теорема. Пусть члены, ряда

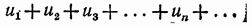
положительны и не возрастают, т. е.

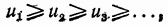
и пусть f(х) - такая непрерывная невозрастсиощая функция, что

Тогда справедливы следующие утверждения:

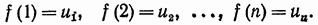
1) если несобственный интеграл сходится (см. § 7 гл. XI т. I), то сходится и ряд (1);

2) если указанный интеграл расходится, то расходится и ряд (1). Доказательство. Изобразим члены ряда геометрически, откладывая по оси абсциссномера членов ряда, а по оси ординат — соответствующие значения членов ряда

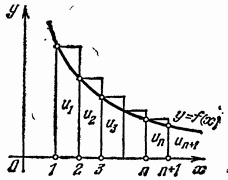
Рис. 360.

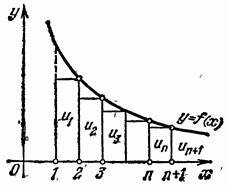
Рис. 361.

Построим на том же чертеже график непрерывной невозрастающей функции

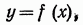
удовлетворяющей условию (2).

Рассматривая рис. 360, замечаем, что первый из построенных прямоугольников имеет основание, равное 1, и высоту 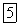Следовательно, площадь этого прямоугольника равна Площадь второго прямоугольника равна и т. д.; наконец, площадь последнего из построенных прямоугольников равна . Сумма площадей построенных прямоугольников равна сумме первых членов ряда. С другой стороны, ступенчатая фигура, образованная этими прямоугольниками, заключает область, ограниченную кривой и прямыми площадь этой области равна Следовательно,

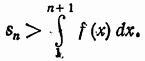
Рассмотрим теперь рис. 361. Здесь первый (слева) из построенных прямоугольников имеет высоту, следовательно, его площадь также равна Площадь второго прямоугольника равна и т. д. Площадь последнего из построенных прямоугольников равна Следовательно, сумма площадей всех построенных прямоугольников равна сумме всех членов 5 ряда, начиная от второго до т. е. равна . С другой стороны, как легко видеть, ступенчатая фигура, образованная этими прямоугольниками, содержится внутри криволинейной фигуры, ограниченной кривой и прямыми . Площадь этой криволинейной фигуры равна . Следовательно,

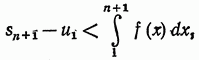
откуда

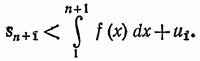
Рассмотрим теперь оба случая.

1) Предположим, что интеграл сходится, т. е. имеет конечное значение.

Так как

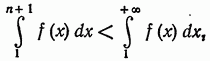
то в силу неравенства (4)

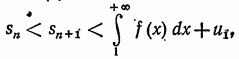
т. e. частичная сумма остается ограниченной при всех значениях n. Но при увеличении она возрастает, так как все члены положительны. Следовательно, при имеет конечный предел т. е. ряд сходится.

2) Предположим далее, что Это значит, что неограниченно возрастает при возрастании . Но тогда

в силу неравенства также неограниченно возрастает при возрастании , т. е. ряд расходится. Таким образом, теорема полностью доказана.

Замечание. Доказанная теорема остается справедливой, если неравенства выполняются, лишь начиная с некоторого N. Пример. Исследовать сходимость ряда

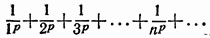
Решение, Применим интегральный признак, положив Эта функция удовлетворяет всем условиям теоремы. Рассмотрим интеграл

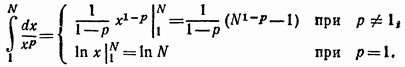
Устремляя N к бесконечности, выясним, сходится ли несобственный интеграл в различных случаях.

На основе этого можно будет судить о сходимости или расходимости ряда при различных значениях

В случае будет т. е. интеграл конечен и, следовательно, ряд сходится;

в случае будет - интеграл бесконечен, ряд расходится;

в случае будет -интеграл бесконечен, ряд расходится, I j