Знакопеременные ряды. Достаточный признак сходимости. Абсолютная и условная сходимость знакопеременного ряда.

Определение 5. Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами.

Ряды, все члены которых отрицательные числа, не представляют нового по сравнению со знакоположительными рядами, так как они получаются умножением знакоположительных рядов на –1.

Изучение знакопеременных рядов начнём с частного случая – знакочередующихся рядов.

Определение 6. Числовой ряд вида u1-u2+u3-u4+…+ +(-1)n-1.un+…, где un – модуль члена ряда, называется знакочередующимся числовым рядом.

Пусть

u1+u2+…+un+…= 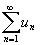(20)

знакопеременный ряд и пусть сходится ряд, составленный из абсолютных величин его членов

│ u1│ +│ u2│ +…+│ un │ +…= 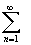│ un │. (21)

Тогда ряд (20) тоже сходится.

Доказательство. Рассмотрим вспомогательный ряд

(u1+│ u1│)+(u2+│ u2│)+…+(un+│ un│)+…= 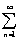(un+│ un│). (22)

Очевидно, 0≤ un+│ un│ ≤ 2│ un│ при всех n=1, 2, …. Ряд (21) сходится по условию, поэтому сходится ряд 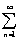2│ un│, тогда по признаку сравнения сходится ряд (22). Ряд (20) представляет собой разность двух сходящихся рядов (22) и (21), поэтому он тоже сходится. Теорема доказана.

Замечание.

Обратное утверждение неверно. Если данный ряд сходится, то ряд, составленный из абсолютных величин его членов, может и расходиться.

Например, ряд 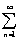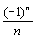сходится по признаку Лейбница, а ряд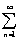 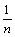расходится (это гармонический ряд).

Теорема.

Если знакопеременный ряд а1+а2+а3+…+ап+… таков, что ряд, составленный из абсолютных величин и его членов 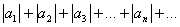сходится, то и данный знакопеременный ряд тоже сходится.

Пример. Исследовать сходимость ряда 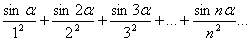, где α – любое число.

Решение. Наряду с данным рядом, рассмотрим ряды

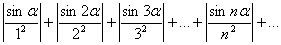
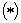
и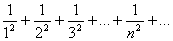

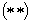
ряд 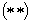сходится как обобщенный гармонический, а члены ряда 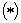не больше соответственных членов ряда 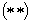, а, значит, по признаку сравнения ряд 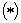также сходится. Но тогда в силу теоремы 1 данный ряд сходится.

Заметим, что признак сходимости, сформулированный в теореме является только достаточным, но не необходимым. Это означает, что существуют такие знакопеременные ряды, которые сами сходятся, а ряды, составленные из абсолютных величин их членов, расходятся. В связи с этим полезно ввести понятия об абсолютной и условной сходимости знакопеременного ряда и на основе этих понятий классифицировать знакопеременные ряды.

Определение.Знакопеременный ряд

а1+а2+а3+…+ап+… (1)

называется абсолютно сходящимся, если сходится ряд

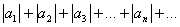(2)

Если же знакопеременный ряд (1) сходится, а ряд (2) расходится, то данный ряд (1) называется условно сходящимся.

Пример 1.

Знакопеременный ряд является условно сходящимся, т.к. ряд, составленный из абсолютных величин его членов, есть гармонический ряд 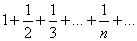, который расходится. А сам данный ряд сходится по теореме Лейбница.

Пример 2.

Знакопеременный ряд 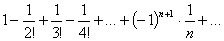является абсолютно сходящимся, т.к. он сходится по теореме Лейбница, а ряд составленный из абсолютных величин его членов 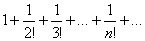будет сходиться по признаку Даламбера. С помощью понятия абсолютной сходимости теорему 1 часто формулируют следующим образом: всякий абсолютно сходящийся ряд есть ряд сходящийся.

В заключении отметим свойства абсолютно и условно сходящихся рядов.

Теорема.

Если ряд сходится абсолютно, то он является абсолютно сходящимся при любой перестановке его членов. При этом сумма ряда не зависит от порядка его членов. Это свойство не сохраняется для условно сходящихся рядов.

Теорема.

Если ряд сходится условно, то какое бы мы ни задали число А, можно переставить его члены, чтобы сумма ряда оказалась равной числу А. Более того, можно так переставить члены условно сходящегося ряда, что ряд, полученный в результате перестановки, окажется расходящимся.