
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Векторами и комплексными числами
|
|
Расчет цепей переменного тока существенно упрощается, если синусоидально изменяющиеся токи, напряжения, ЭДС и другие величины заменить их изображениями на комплексной плоскости (рис. 3.2)

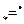
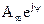
 |
где
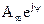 - называется комплексной амплитудой.
- называется комплексной амплитудой.
Комплексная амплитуда представляет собой вектор на комплексной плоскости, длина которого соответствует амплитудному значению синусоидальной функции Аm, а угол ψ – начальной фазе.
В курсе ТОЭ пользуются следующими темя формами записи комплексной амплитуды в виде комплексного числа:
показательная 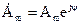 ;
;
тригонометрическая 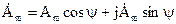 ;
;
алгебраическая 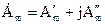 .
.
где 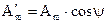 - действительная часть комплексного числа;
- действительная часть комплексного числа;
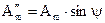 - мнимая часть комплексного числа,
- мнимая часть комплексного числа,
Для обратного перехода от алгебраической к показательной форме записи необходимо найти модуль этого комплексного числа с помощью теоремы Пифагора (рис.3.2) и аргумент путем определения тангенса соответствующего угла:
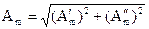 ,
, 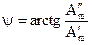 .
.
Алгебраическая форма удобна при сложении и вычитании комплексных величин, а показательная при умножении, делении, возведении в степень и извлечении корня.
Мнимая единица 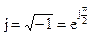 называется оператором поворота на угол
называется оператором поворота на угол 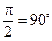 . Умножение на
. Умножение на 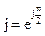 сводится к повороту вектора против часовой стрелки на прямой угол, а умножение на
сводится к повороту вектора против часовой стрелки на прямой угол, а умножение на  - к повороту вектора на прямой угол по часовой стрелке.
- к повороту вектора на прямой угол по часовой стрелке.
Числа 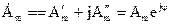 и
и 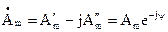
называют комплексно-сопряженными числами. Произведение комплексно-сопряженных чисел - действительное число, равное квадрату их модуля 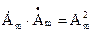 .
.
Комплексное действующее значение 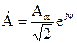 .
.
 |
Все формы записи комплексной величины и связь между ними записываются
Векторная диаграмма представляет собой совокупность векторов токов и напряжений, построенных на комплексной плоскости.