
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Последовательное соединение элементов R, L, C
|
|
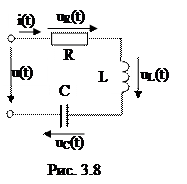
Пусть в цепи, состоящей из последовательно соединенных элементов R, L, C (рис. 3.8), известен ток i(t)=Imsin(ω t +ψ i) и необходимо определить напряжение на ее зажимах.
Запишем для цепи уравнение по второму закону Кирхгофа для мгновенных значений напря-жений:
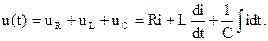
Сумме синусоидальных напряжений соответствует сумма изображающих их комплексных величин. Тогда для действующих комплексных значений можно записать
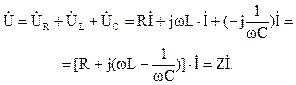 Величину
Величину 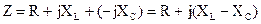
называют комплексным сопротивлением цепи с последова-тельным соединением элементов R, L, C. Заметим, что в этом случае комплексные сопротивления отдельных участков цепи складываются, как и сопротивления цепи постоянного тока.
Запишем комплексное сопротивление в показательной форме:
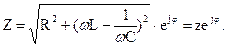
Модуль комплексного сопротвления
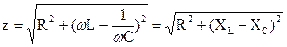 называют полным сопротивлением цепи.
называют полным сопротивлением цепи.
Аргумент комплексного сопротивления
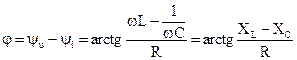 - угол сдвига фаз между входным напряжением и током; сдвиг фаз определяется соотношением реактивных и активных сопротивлений, включенных в электрическую цепь.
- угол сдвига фаз между входным напряжением и током; сдвиг фаз определяется соотношением реактивных и активных сопротивлений, включенных в электрическую цепь.
При  угол φ > 0, ток отстает по фазе от напряжения. При
угол φ > 0, ток отстает по фазе от напряжения. При 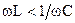 угол φ < 0, ток опережает напряжение по фазе. При
угол φ < 0, ток опережает напряжение по фазе. При 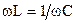 угол φ =0, ток совпадает по фазе с напряжением и цепь ведет себя как чисто активное сопротивление. Такой режим работы цепи называют режимом резонанса напряжений.
угол φ =0, ток совпадает по фазе с напряжением и цепь ведет себя как чисто активное сопротивление. Такой режим работы цепи называют режимом резонанса напряжений.
Построим векторные диаграммы тока и напряжений на участках цепи с последовательным соединением элементов R, L, C. При построении векторных диаграмм примем начальную фазу тока равной нулю, ψ i=0. Тогда сдвиг фаз φ между входным напряжением и током и начальная фаза входного напряжения ψ u будут равны друг другу. Напряжение 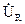 на активном сопротивлении совпадает по фазе c током, напряжение на индуктивном элементе
на активном сопротивлении совпадает по фазе c током, напряжение на индуктивном элементе 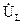 опережает ток на 90°, напряжение на емкостном элементе
опережает ток на 90°, напряжение на емкостном элементе 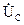 отстает от тока по фазе на 90°.
отстает от тока по фазе на 90°.
В соответствии с тремя возможными вариантами соотношения между реактивными сопротивлениями XL и XC (XL> XC, XL< XC, XL = XC) построим три векторные диаграммы для каждого из случаев (рис. 3.9, а, б, в).
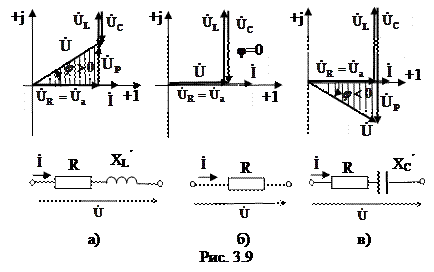
Как известно, на векторных диаграммах угол сдвига фаз φ отсчитывается от вектора тока  к вектору напряжения
к вектору напряжения  . Угол φ положителен при отстающем токе (рис. 3.9, а) и отрицателен при опережающем токе (рис. 3.9, в).
. Угол φ положителен при отстающем токе (рис. 3.9, а) и отрицателен при опережающем токе (рис. 3.9, в).
Заштрихованные треугольники, показанные на векторных диаграммах, принято называть треугольниками напряжений. Проекцию вектора напряжения на направление вектора тока называют активной составляющей напряжения и обозначают  . Проекцию вектора напряжения на направление, перпендикулярное вектору тока, называют реактивной составляющей напряжения и обозначают
. Проекцию вектора напряжения на направление, перпендикулярное вектору тока, называют реактивной составляющей напряжения и обозначают 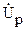 .
.
Из векторных диаграмм рис. 3.9 видно, что:
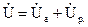
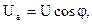
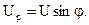
При неизменной частоте источника питания цепь рис. 3.8 может быть представлена одной из эквивалентных схем, представленных на рис. 3.9, а, б, в: при XL> XC как последовательное соединение активного и индуктивного сопротивлений (R и XL´ =XL-XC); при XL=XC как активное сопротивление R; при XL< XC как последовательное соединение активного и емкостного сопротивлений (R и XС´ =XL-XC).
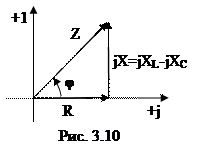 Если каждую сторону треугольника напряжений поделить на вектор тока, то получим треугольник, подобный исходному и называемый треугольником сопротивлений (рис. 3.10).
Если каждую сторону треугольника напряжений поделить на вектор тока, то получим треугольник, подобный исходному и называемый треугольником сопротивлений (рис. 3.10).