
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример. Канал может находиться в трех состояниях
|
|
Канал может находиться в трех состояниях. Последовательность состояний является простой цепью Маркова. Какое число переходных вероятностей необходимо знать для задания модели канала? - 9.
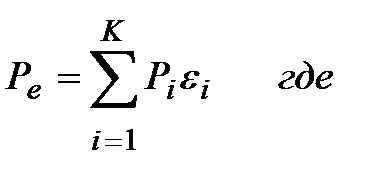
Средняя вероятность ошибочного приема двоичного символа в канале с К состояниями определяется по формуле
Рi – финальные, то есть безусловные вероятности состояний канала в произвольный момент времени i. Финальные вероятности определяются из системы уравнений:
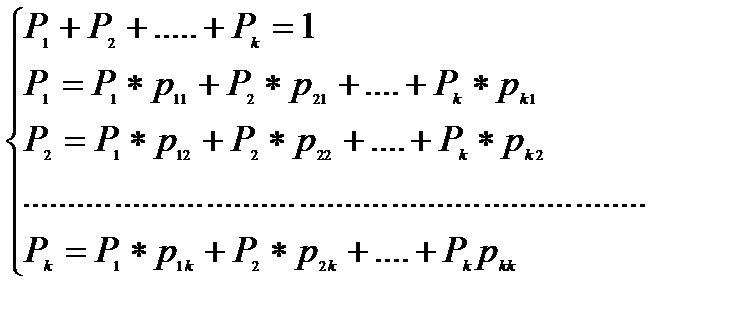
Тогда средняя вероятность ошибки в двоичном символе для такого канала равна Pe=P1 1+P2 2+…+Pk k.
Средняя вероятность безошибочного приема двоичного символа равна
Q=1-Pe.
Модели дискретных каналов
Несоответствие принятого элемента сигнала данных переданному называется ошибкой.
С. целью аналитического моделирования систем ПДС проведены многочисленные исследования закономерности потоков ошибок и предложен ряд математических моделей дискретных каналов [5]. При этом к моделям источника ошибок предъявляются следующие требования: удобство аналитического моделирования систем ПДС, обеспечивающее достаточное соответствие модели систем и реальным объектам; простота оценки параметров модели в результате измерений.
Модель дискретных каналов может строиться двумя способами, Если при первом способе применяются существующие математическиe модели случайных процессов и экспериментально оценивается достаточно большое число их параметров, то при втором используются аппроксимационные способы представления потока ошибок. В случае, когда ошибки в каналах появляются независимо с вероятностью рош, вероятность появления в n-элементной комбинации t ошибок P(t, n) определяется биномиальным распределением!
р (t, n)= 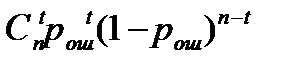
При этом вероятность приема неискаженной комбинации (t=0),
Р (0, n)= 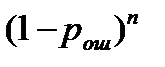 ,
,
а вероятность появления хотя бы одной ошибки (рис. 1.6)
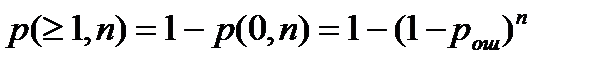 .
.
Вероятность появления т и более ошибок
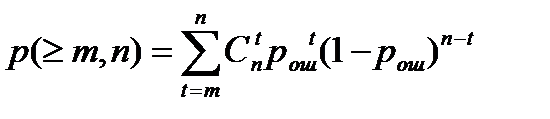
Для большинства каналов данная модель приводит к недопустимым погрешностям. В соответствии с моделью Гильберта, учитывающей группирование ошибок, канал может находиться в одном из двух состояний — «хорошем», когда ошибки невозможны, и «плохом», когда возникают независимые ошибки с вероятностью 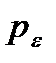 . Канал задается матрицей переходных вероятностей
. Канал задается матрицей переходных вероятностей
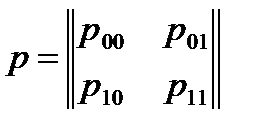
(1.21)
и вероятностью 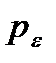 . Вероятность ошибки в канале
. Вероятность ошибки в канале
p ош = 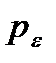 p 10/(p 01+ p 10).(1.22)
p 10/(p 01+ p 10).(1.22)
Вероятность возникновения пакета ошибок с данного элемента
p п == p 01 p 10/(p 01+ p 10).
Другой распространенной моделью является модель В. Беннета и Ф. Фройлиха, которая задается тремя параметрами:
вероятностью появления пакета рп, равной отношению чиcла пакетов к общему числу переданных бит; пакеты независимы;;
распределением вероятностей пакетов рп(l) различной длины l;
вероятностью ошибки в пакете рош.п.
Простейшей моделью, учитывающей группирование ошибок в пакеты, является модель Бергера — Мандельброта.
Обобщением модели Беннета-Фройлиха является модель Попова — Турина, которая предполагает существование в канале независимо возникающих цепочек пакетов ошибок. Распределение длин цепочек полагается геометрическим. Внутри цепочек независимо появляются пакеты ошибок, длины которых распределены по полигеометрическому закону. Внутри пакетов задается условная вероятность появления ошибок.
Задача 1.20. Определить вероятность Р (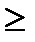 1, n) ошибочного приема для каналов с независимыми ошибками кодовой последовательности длиной n =9 для р ош=1•10-3 и 1•10-5.
1, n) ошибочного приема для каналов с независимыми ошибками кодовой последовательности длиной n =9 для р ош=1•10-3 и 1•10-5.
Решение. Вероятность Р (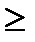 1, n) = 1—(1— Р ош)n
1, n) = 1—(1— Р ош)n 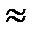 np ош = 9•10-3 и 9•10-5
np ош = 9•10-3 и 9•10-5
Задача 1.21. Определить для тех же условий вероятности приема неискаженной комбинации P(Q, п), а также вероятности появления т=2,..., 5 и более.
Рассмотрим двухпараметрическую модель дискретного канала Л. П. Пуртова [49, 71]. Вероятность появления искажений кодовой комбинации длиной п (см. рис. 1.6)
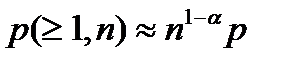 при пр < < 1.
при пр < < 1.
При а 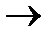 0 имеем случай независимого появления ошибок, а при а
0 имеем случай независимого появления ошибок, а при а 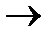 1 — появления групповых ошибок (при а= 1 вероятность искажений комбинации не зависит от n, так как в каждой ошибочной комбинации все элементы приняты с ошибкой). Поэтому а является показателем группирования. Для реальных каналов а=0, 3...... 0, 7, а р=10-3... 10-5. Распределение ошибок суммарной кратности в комбинациях разной длины
1 — появления групповых ошибок (при а= 1 вероятность искажений комбинации не зависит от n, так как в каждой ошибочной комбинации все элементы приняты с ошибкой). Поэтому а является показателем группирования. Для реальных каналов а=0, 3...... 0, 7, а р=10-3... 10-5. Распределение ошибок суммарной кратности в комбинациях разной длины
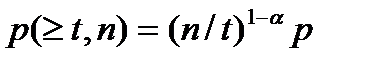 .
.
Задача 1.24. При передаче дискретных сообщений по KB радиотелеграфному каналу блоками длиной 127 элементов определить вероятность появления в блоке четырех и более ошибок, если известны р=1, 31•10-2 и а=0, 448.
Решение. Вероятность.
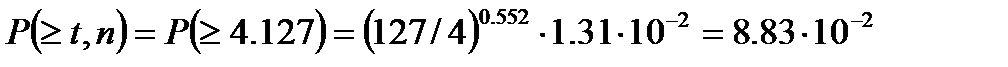
Рассмотренные модели источников ошибок не учитывают нестационарность потока ошибок в каналах {часовые, дневные и недельные вариации). Поэтому с точки зрения адекватности модели реальным каналам наиболее перспективной следует считать модель дискретного канала с переменными параметрами [5.35]
Дополнительная литература 2[ 58-66], 6 [73-80].
Контрольные вопросы:
1. Модель канала с памятью
2. Модель канала без памятью
3. Симметричный канал.
4. Модель Маркова.
5. Модель Гильберта.
Лекция №7 (2 час.)