
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Импульсы Найквиста
|
|
Рассмотрим последовательность информационных импульсов на входе передатчика и последовательность импульсов, получаемую на выходе согласованного фильтра с характеристикой типа приподнятого косинуса (перед дискретизацией). На рис. 3.21 переданные данные представлены импульсными сигналами, которые появляются в мо- менты времени 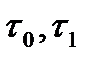 ,.... Фильтрование приводит к расширению входных сигналов, а следовательно, к запаздыванию их во времени. Время поступления импульсов обозначим t0, , t1.... Импульс, переданный в момент времени т0, поступает в приемник в момент времени t0. Хвост, предшествующий основному лепестку демодулированного импульса, называется его предтечей (precursor). Для реальной системы с фиксированным системным эталонным временем принцип причинности предписывает условие t0
,.... Фильтрование приводит к расширению входных сигналов, а следовательно, к запаздыванию их во времени. Время поступления импульсов обозначим t0, , t1.... Импульс, переданный в момент времени т0, поступает в приемник в момент времени t0. Хвост, предшествующий основному лепестку демодулированного импульса, называется его предтечей (precursor). Для реальной системы с фиксированным системным эталонным временем принцип причинности предписывает условие t0 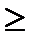
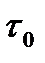 , а разность времен
, а разность времен 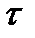 0 - t0 выражает задержку распространения в системе. В данном примере интервал времени от начала предтечи демодулированного импульса и до появления его главного лепестка или максимальной амплитуды равен 3Т (утроенное время передачи импульса). Каждый выходящий импульс последовательности накладывается на другие импульсы; каждый импульс воздействует на основные лепестки трех предшествующих и трех последующих импульсов. В подобном случае, когда импульс фильтруется (формируется) так, что занимает более одного интервала передачи символа, определяется параметр, называемый временем поддержки (support time) импульса. Время поддержки — это количество интервалов передачи символа в течение длительности импульса. На рис. 3.21 время поддержки импульса равно 6 интервалам передачи символа (7 информационных точек с 6 интервалами между ними).
0 - t0 выражает задержку распространения в системе. В данном примере интервал времени от начала предтечи демодулированного импульса и до появления его главного лепестка или максимальной амплитуды равен 3Т (утроенное время передачи импульса). Каждый выходящий импульс последовательности накладывается на другие импульсы; каждый импульс воздействует на основные лепестки трех предшествующих и трех последующих импульсов. В подобном случае, когда импульс фильтруется (формируется) так, что занимает более одного интервала передачи символа, определяется параметр, называемый временем поддержки (support time) импульса. Время поддержки — это количество интервалов передачи символа в течение длительности импульса. На рис. 3.21 время поддержки импульса равно 6 интервалам передачи символа (7 информационных точек с 6 интервалами между ними).
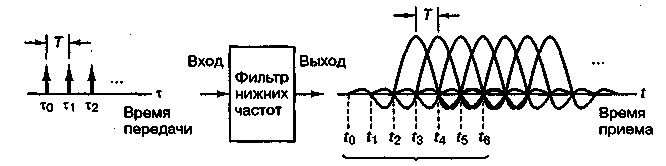
Время поддержки импульса Рис.8.2. Фильтрованная последовательность импульсов: выход и вход
На рис. 8.2, а показан импульсный отклик фильтра с характеристикой типа корня из приподнятого косинуса (максимальное значение нормированного фильтра равно единице, коэффициент сглаживания фильтра r = 0, 5), а на рис. 8.22, б изображен импульсный отклик фильтра с характеристикой типа приподнятого косинуса, называемый импульсом Найквиста (нормирование и значение коэффициента сглаживания такие же, как и на рис. 3.22, а). Изучая эти два импульса, можно заметить, что они очень похожи. Однако первый имеет несколько более частые переходы, а значит, его спектр (корень квадратный из приподнятого косинуса) не так быстро затухает, как спектр (приподнятый косинус) импульса Найквиста. Еще одним малозаметным, но важным отличием является то, что импульс Найквиста с характеристикой типа корня из приподнятого косинуса не дает нулевой межсимвольной интерференции (можно проверить, что хвосты импульса на рис. 8.22, а не проходят через точку нулевой амплитуды в моменты взятия выборок). В то же время, если фильтр с характеристикой типа корня из приподнятого косинуса используется и в передатчике, и в приемнике, произведение передаточных функций двух фильтров дает характеристику типа приподнятого косинуса, что означает нулевую межсимвольную интерференцию на выходе.
Было бы неплохо рассмотреть, как импульсы Найквиста с характеристикой типа корня из приподнятого косинуса выглядят на выходе передатчика и какую форму они имеют после демодуляциисфильтром, характеристика которого также представляет собой корень из приподнятого
На рис. 8.23, а в качестве примера передачи приведена последовательность символов сообщения {+1 +1 -1 +3 +1 +3} из четверичного набора символов, где алфавит состоит из символов {±1, ±3}. Будем считать, что импульсы модулируются с помощью четверичной кодировки РАМ, а их форма определяется фильтром с характеристикой типа корня из приподнятого косинуса с коэффициентом сглаживания r = 0, 5. Аналоговый сигнал на рис. 3.23, а описывает выход передатчика. Сигнал на выходе (последовательность импульсов Найквиста, форма которых получена с выхода фильтра с характеристикой типа корня из приподнятого косинуса) запаздывает относительно сигнала на входе (показанного в виде импульсов), но для удобства визуального представления, чтобы читатель мог сравнить выход фильтра с его входом, оба сигнала изображены как одновременные. В действительности передается (или модулируется) только аналоговый сигнал.
На рис. 8.23, б показаны те же задержанные символы сообщения, а также сигнал с выхода согласованного фильтра с характеристикой типа корня из приподнятого.
Исследованием проблемы задания формы принятого импульса с тем, чтобы предотвратить появление ISI на детекторе, долгое время занимался Найквист [6]. Он показал, что минимальная теоретическая ширина полосы системы, требуемая для детектирования 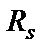 символов/секунду без ISI, равна
символов/секунду без ISI, равна 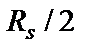 Гц. Это возможно, если передаточная функция системы
Гц. Это возможно, если передаточная функция системы 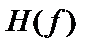 имеет прямоугольную форму, как показано на рис. 8.16, а. Для низкочастотных систем с такой
имеет прямоугольную форму, как показано на рис. 8.16, а. Для низкочастотных систем с такой 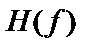 , что односторонняя ширина полосы фильтра равна
, что односторонняя ширина полосы фильтра равна 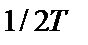 (идеальный фильтр Найквиста), импульсная характеристика функции
(идеальный фильтр Найквиста), импульсная характеристика функции 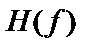 , вычисляемая с помощью обратного преобразования Фурье (см. табл. А.1), имеет вид
, вычисляемая с помощью обратного преобразования Фурье (см. табл. А.1), имеет вид 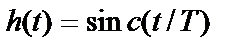 ; она показана на рис. 3.16, б. Импульс, описываемый функцией
; она показана на рис. 3.16, б. Импульс, описываемый функцией 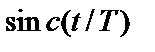 , называется идеальным импульсом Найквиста; он имеет бесконечную длительность и состоит из многочисленных лепестков: главного и боковых, именуемых хвостами.
, называется идеальным импульсом Найквиста; он имеет бесконечную длительность и состоит из многочисленных лепестков: главного и боковых, именуемых хвостами.
косинуса. 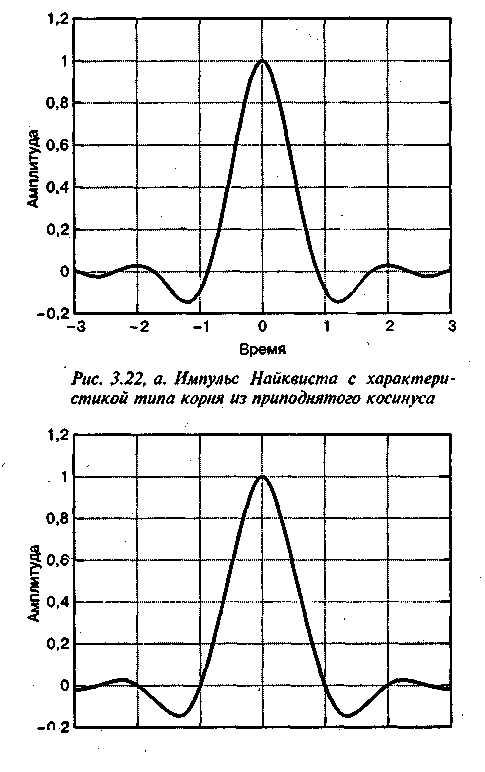
-3 -2 -1 0. 1 2 3
Время
Рис.8.22, б. Импульс Найквиста с характеристикой типа приподнятого косинуса
Поскольку ограничение ширины полосы по Найквисту устанавливает теоретическое максимальное уплотнение скорости передачи символов без межсимвольной интерференции, равное 2 символа/с/Гц, может возникнуть вопрос, можно ли что-то сказать об ограничении величин, измеряемых в бит/с/Гц. О последних ничего нельзя сказать прямо; ограничение связано только с импульсами или символами и возможностью детектирования их амплитудных значений без искажения со стороны других импульсов. При нахождении 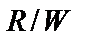 длялюбой схемы передачи сигналов необходимо знать, сколько битов представляет каждый символ, что само по себе является темой отдельного рассмотрения. Допустим, сигналы кодируются с использованием М -уровневой кодировки РАМ. Каждый символ (включающий
длялюбой схемы передачи сигналов необходимо знать, сколько битов представляет каждый символ, что само по себе является темой отдельного рассмотрения. Допустим, сигналы кодируются с использованием М -уровневой кодировки РАМ. Каждый символ (включающий 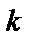 бит) представляется одной из М импульсных амплитуд. Для
бит) представляется одной из М импульсных амплитуд. Для 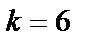 бит на символ размер набора символов составляет
бит на символ размер набора символов составляет  амплитуды. Таким образом, при 64-уровневой кодировке РАМ теоретическая максимальная эффективность использования полосы, не допускающая межсимвольной интерференции, равна 12 бит/с/Гц. (Подробнее об эффективности использования полосы в главе
амплитуды. Таким образом, при 64-уровневой кодировке РАМ теоретическая максимальная эффективность использования полосы, не допускающая межсимвольной интерференции, равна 12 бит/с/Гц. (Подробнее об эффективности использования полосы в главе
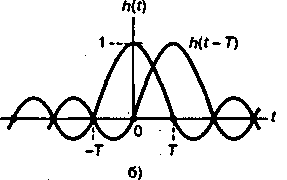
Найквист установил, что если каждый импульс принятой последовательности имеет вид 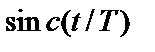 , импульсы могут детектироваться без межсимвольной интерференции. На рис. 3.16, б показано, как удается обойти ISI. Итак, имеем два последовательных импульса,
, импульсы могут детектироваться без межсимвольной интерференции. На рис. 3.16, б показано, как удается обойти ISI. Итак, имеем два последовательных импульса, 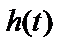 и
и 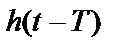 . Несмотря на то что хвосты функции
. Несмотря на то что хвосты функции 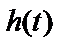 имеют бесконечную длительность, из рисунка видно, что в момент
имеют бесконечную длительность, из рисунка видно, что в момент 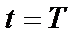 взятия выборки функции
взятия выборки функции 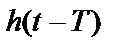 хвост функции
хвост функции 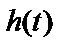 проходит через точку нулевой амплитуды, и подобным образом он будет иметь нулевую амплитуду в моменты взятия выборок всех остальных импульсов последовательности
проходит через точку нулевой амплитуды, и подобным образом он будет иметь нулевую амплитуду в моменты взятия выборок всех остальных импульсов последовательности 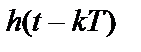 ,
, 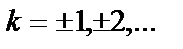 . Следовательно, предполагая идеальную синхронизацию процесса взятия выборок, получаем, что межсимвольная интерференция не будет влиять на процесс детектирования. Чтобы низкочастотная система могла детектировать
. Следовательно, предполагая идеальную синхронизацию процесса взятия выборок, получаем, что межсимвольная интерференция не будет влиять на процесс детектирования. Чтобы низкочастотная система могла детектировать  таких импульсов (символов) в секунду, ширина ее полосы должна быть равна
таких импульсов (символов) в секунду, ширина ее полосы должна быть равна 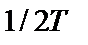 ; другими словами, система с шириной полосы
; другими словами, система с шириной полосы 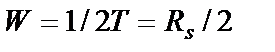 Гц может поддерживать максимальную скорость передачи
Гц может поддерживать максимальную скорость передачи 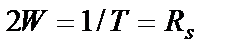 символов/с (ограничение полосы по Найквисту) без ISI. Следовательно, при идеальной фильтрации Найквиста (и нулевой межсимвольной интерференции) максимальная возможная скорость передачи символов на герц полосы, называемая уплотнением скорости передачи символов (symbol-rate packing), равна
символов/с (ограничение полосы по Найквисту) без ISI. Следовательно, при идеальной фильтрации Найквиста (и нулевой межсимвольной интерференции) максимальная возможная скорость передачи символов на герц полосы, называемая уплотнением скорости передачи символов (symbol-rate packing), равна
2 символа/с/Гц. Вследствие прямоугольной формы передаточной функции идеального фильтра Найквиста и бесконечной длины соответствующего импульса, подобные идеальные фильтры нереализуемы; реализовать их можно только приближенно.
а)
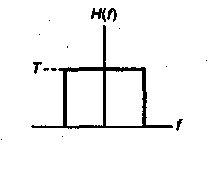
Рис. 8.16. Каналы Найквиста для нулевой межсимвольной интерференции: а) прямоугольная передаточная функция системы 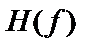 ; б) принятый импульс
; б) принятый импульс 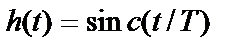
Стоит отметить, что названия " фильтр Найквиста" и " импульс Найквиста" часто используются для описания обширного класса фильтраций и импульсных форм, удовлетворяющих условию нулевой межсимвольной интерференции в точках взятия выборок. Фильтр Найквиста — это фильтр, передаточная функция которого может быть представлена прямоугольной функцией, свернутой с любой четно-симметричной частотной функцией. Импульс Найквиста — это импульс, форма которого может быть описана функцией 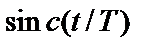 , умноженной на другую временную функцию. Следовательно, существует бесконечное множество фильтров Найквиста и соответствующих импульсов. В классе фильтров Найквиста наиболее популярными являются фильтры с характеристикой типа приподнятого косинуса или корня из приподнятого косинуса. Несколько позже эти фильтры будут рассмотрены подробно.
, умноженной на другую временную функцию. Следовательно, существует бесконечное множество фильтров Найквиста и соответствующих импульсов. В классе фильтров Найквиста наиболее популярными являются фильтры с характеристикой типа приподнятого косинуса или корня из приподнятого косинуса. Несколько позже эти фильтры будут рассмотрены подробно.
Основным параметром систем связи является эффективность использования полосы, 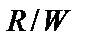 , измеряемая в бит/с/Гц. Как можно понять из единиц измерения,
, измеряемая в бит/с/Гц. Как можно понять из единиц измерения, 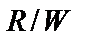 представляет меру скорости переноса данных на единицу ширины полосы, а значит, показывает, насколько эффективно любой метод передачи сигналов использует ресурс полосы.
представляет меру скорости переноса данных на единицу ширины полосы, а значит, показывает, насколько эффективно любой метод передачи сигналов использует ресурс полосы.