Fig.8 The transient processes of control systems.

This general solution has the following form:

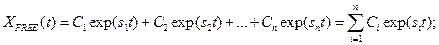(1.23)

where:

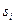- the roots of system characteristic equation ;

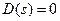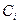- integration constants which are defined by initial conditions.

Thus, Eq.(1.23) describes a transient process - the system free movement.

A linear control system whose transient process represents the oscillation damping in the course of time (when the amplitude of 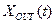is continuously diminishing) is called a stable control system according to the following condition:

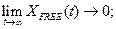(1.24)

If the condition Eq.(1.24) isn’t satisfied then we obtain an unstable control system with the un-damped transient process.

B. The particular solution – the system forced movement component.

The 2^nd component solution describes the system forced movement in steady-state regime.

We assume that a forced input action is a harmonic function:

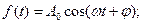(1.25)

where:

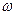- a circular frequency of oscillation;

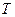- a period of oscillation;

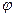- a phase shift.

We assume that the phase shift is equal to 0, in this case the input harmonic action will be:

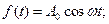(1.26)