Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
FIGURE 4.7 RLC circuit.
|
|
Alternatively, one may describe the electrical RLC circuit of Figure 4.7 by utilizing Kirchhoffs current law. Then we obtain the following integro-differential equation:
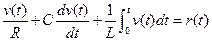 (4.33)
(4.33)
The solution of the differential equation describing the process may be obtained by classical methods such as the use of integrating factors and the method of undetermined coefficients. For example, when the mass is initially displaced a distance 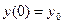 and released, the dynamic response of an under-damped system is represented by an equation of the form
and released, the dynamic response of an under-damped system is represented by an equation of the form
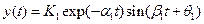 (4.34)
(4.34)
A similar solution is obtained for the voltage of the RLC circuit when the circuit
is subjected to a constant current r(t) = I. Then the voltage is
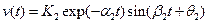 (4.35)
(4.35)
A voltage curve typical of an under-damped RLC circuit is shown in Figure 2.4.
To reveal further the close similarity between the differential equations for the mechanical and electrical systems, we shall rewrite Equation (4.32) in terms of velocity:
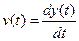
Then we have
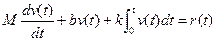 (4.36)
(4.36)