Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Example 2
|
|

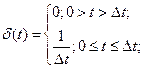 (4.31)
(4.31)
If impulse area is equal to s, then we consider that we have S-scale impulse of 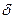 -function which is equal to
-function which is equal to 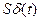 .
.
The system reaction to 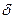 -function is called impulse transient characteristic (impulse response), or weighting function
-function is called impulse transient characteristic (impulse response), or weighting function 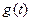 .
.
Together with transient characteristic it is the most important characteristic of system dynamic properties.
If we have a time shift 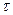 , then
, then 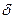 -function will have the following form:
-function will have the following form:
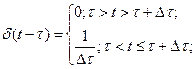 (4.32)
(4.32)
Signals in the form of impulse functions may be considered as derivatives of unit step function 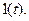
Taking into account an order of a derivative we obtain:
- 1st order impulse function or 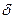 -function;
-function;
- 2nd order impulse function, …
To prove this statement we may represent the unit step function 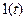 as the limit of a certain continuous function:
as the limit of a certain continuous function:
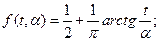 (4.33)
(4.33)
Within the interval 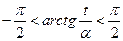 we may obtain:
we may obtain:
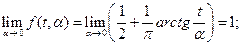 (4.34)
(4.34)
The derivative of the unit step function:
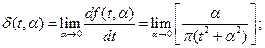 (4.35)
(4.35)
Thus, we obtain:
- 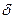 -function = 0 at
-function = 0 at 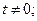
- 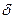 -function =
-function = 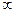 at
at 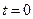 ;
;
- if 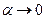 then
then 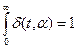 .
.
This interpretation is convenient, since it allows to obtain analytical expressions for 2nd, 3rd, …, k-th order impulse functions.
Their expressions and graphic forms may be obtained as the limits of derivatives of 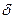 -functions at
-functions at 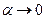 according to Eq.(5.8).
according to Eq.(5.8).
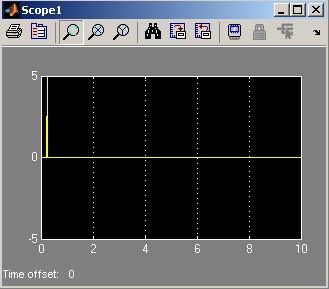
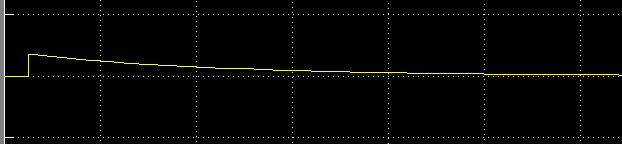
You may construct 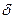 -function block using the following blocks from Matlab6.5:
-function block using the following blocks from Matlab6.5:
- Step;
- Derivative (du/dt).
The connection between transient characteristic and weighting function may be also established using two step functions.
|