FIGURE 4.4 Graphical evaluation of the residues.

The graphical representation of Equation (4.23) is shown in Figure 4.3. The graphical method of evaluating the residues is particularly valuable when the order of the characteristic equation is high and several poles are complex conjugate pairs.

The inverse Laplace transform of Equation (4.20) is then

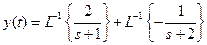(4.24)

Using Table 1, we find that

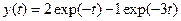(4.25)

Finally, it is usually desired to determine the steady-state or final value of the response of y(t). For example, the final or steady-state rest position of the spring-mass-damper system may be calculated. The final value theorem states that

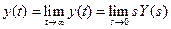(4.26)

where a simple pole of Y(s) at the origin is permitted, but poles on the imaginary axis and in the right half-plane and repeated poles at the origin are excluded. Therefore, for the specific case of the spring-mass-damper system, we find that

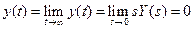(4.27)

Hence the final position for the mass is the normal equilibrium position .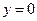

Further consideration requires to study the properties of the spring-mass-damper system.