
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Концепція оцінки вартості грошей у часі
|
|
Прийняття рішення про вкладення капіталу визначається величиною доходу, який інвестор передбачає отримати у майбутньому. Наприклад, купуючи зараз облігацію, ми розраховуємо протягом у всього строку позики отримувати доход у вигляді нарахованих відсотків, а із закінченням строку позики - повернути вкладені кошти. У даному прикладі інвестиційний доход дорівнює сумі отриманих відсотків і вкладених коштів, однак позитивні грошові потоки (відсотки і повернені кошти) і негативні грошові потоки (інвестування капіталу) не будуть співпадати у часі виникнення, тобто будуть не співставленні.
Часова теорія вартості грошей виходить з припущення, що гроші, будучи специфічним товаром, з часом змінюють свою вартість і зазвичай знецінюються. Змінення з часом вартості грошей відбувається під впливом цілого ряду факторів. Найважливішими такими факторами можна назвати не тільки інфляцію, але й здатність грошей приносити доход.
Таким чином, у розглянутому прикладі необхідно порівнювати витрати на придбання облігацій з сумою наступних доходів, приведених за вартістю до моменту інвестування.
Концепція вартості грошей у часі полягає у тому, що вартість грошей протягом часу змінюється с урахуванням норми прибутку на фінансовому ринку, у якості якої, зазвичай, виступає норма позикового відсотку.
У процесі порівняння вартості грошових коштів при їх інвестуванні і поверненні прийнято використовувати два поняття - наступну і поточну вартість грошей.
Приведення грошових сум, які виникають у різний час, до порівняльного виду називається «часовою оцінкою грошових потоків».
Грошовий потік - це грошові надходження чи платежі, які породжуються проектом на окремих кроках протягом розрахункового періоду.
Часова оцінка грошових потоків основана на використанні шести функцій:
- Складний відсоток.
- Дисконтування.
- Поточна вартість ануїтету.
- Періодичний внесок у погашення кредиту.
- Періодичний внесок у фонд нагромадження.
- Наступна вартість ануїтету.
Теорія і практика використання функцій складного відсотку базується на ряді понять і допущень:
- Грошовий потік представляє собою платежі, які виникають у визначеній хронологічній послідовності.
- Грошовий потік, у якому платежі відрізняються за величиною чи не постійні у часі, називаються «звичайним грошовим потоком».
- Грошовий потік рівних платежів, які виробляються через фіксовані інтервали часу протягом заданого строку, називаються ануїтетом.
Функція «складний відсоток»
Функція «складний відсоток» дозволяє визначити наступну вартість суми, яку має інвестор у теперішній час, виходячи з передбаченої ставки доходу, строку накопичення і періодичності нарахування відсотків.
При одноразовому внеску розрахунок наступної вартості здійснюється за формулою складного відсотку
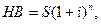
де НВ - наступна вартість (величина накопичення); S - первісний внесок; i - відсоткова ставка; n - число періодів нарахування відсотків.
Множник 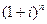 - називають коефіцієнтом компадування.
- називають коефіцієнтом компадування.
Приклад. Інвестора цікавить не просто величина капітальних витрат на реалізацію інвестиційного проекту, а параметри позитивних і негативних грошових потоків, зокрема величина і час окремих платежів.
Будівельна компанія пропонує збудувати об'єкт за один рік вартістю 1 млн. грн., але для інвестора цієї інформації недостатньо. Інвестор має знати коли треба буде зробити необхідні витрати.
Якщо ці витрати будуть зроблені у момент закінчення будівництва об’єкту, то його вартість дійсно буде дорівнювати 1 млн. грн. Якщо сплату треба буде виробити за рік до закінчення будівництва, справжня вартість об’єкту буде дорівнювати 1 млн. грн. плюс відсоток на вкладений мільйон за рік (наприклад, ці кошти можуть бути вкладені на один рік у комерційний банк на депозит під 15% річних).
Задача. Яка сума буде накопичена вкладником через три роки, якщо первісний внесок складає 400 тис. грн., відсотки нараховуються щорічно по ставці 10% і з обігу не вилучаються?
Рішення. Розрахуємо суму накопичення
НВ = 400(1 + 0, 1)(1 + 0, 1)(1 + 0, 1) = 400  1, 1
1, 1  1, 1
1, 1  1, 1 = 400
1, 1 = 400  1, 331 = 532, 4 тис. грн.
1, 331 = 532, 4 тис. грн.
Суми, накопичені за роками, виставлені у табл. 3.1.
Таблиця 3.1
Процес накопичення у динаміці
| Рік | НВ, тис. грн. |
| Перший Другий Третій |
400  1, 1 = 440
440 1, 1 = 440
440  1, 1 = 484
484 1, 1 = 484
484  1, 1 = 532, 4 1, 1 = 532, 4
|
Таким чином, складний відсоток припускає нарахування відсотків не тільки на суму первісного внеску, але й на суму відсотків, які накопичені до кінця кожного періоду. Це можливо тільки у випадку реінвестування суми нарахованих відсотків, тобто поєднання їх з інвестиційним капіталом.
Якщо відсотки, які нараховані до кінця кожного періоду, вилучаються чи відсоток нараховується один раз у кінці депозитного договору, то розрахунок наступної вартості здійснюється за формулою простого відсотку
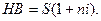
Якщо приведена раніше ситуація припускала б нарахування простого відсотку, то накопичена сума склала б 400(1 + 3  0, 1) = 520 тис. грн., тобто на 12, 4 тис. грн. менше.
0, 1) = 520 тис. грн., тобто на 12, 4 тис. грн. менше.
При багаторазових внесках розрахунок наступної вартості здійснюється за формулою
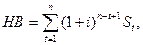
де t - номер внеску; 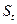 - внесок за рахунком t.
- внесок за рахунком t.
Задача. Вкладник припускає вкладати під 10% річних протягом трьох років наступні суми: у перший рік - 100 тис. грн., у другий - 80 тис. грн., у третій - 120 тис. грн. Яка сума буде накопичена вкладником у кінці третього року?
Рішення.
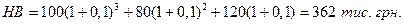
Задача. Перед інвестором виникла задача розмістити 100 тис. грн. на депозитний внесок строком на один рік. Один банк пропонує інвестору виплачувати доход з складних відсотків у розмірі 23% у квартал; другий - у розмірі 30% один раз у чотири місяці; третій - у розмірі 45% два рази на рік; четвертий - у розмірі 100% один раз на рік. Визначте найбільш доходний варіант інвестування.
Рішення. Для визначення, який варіант інвестування найбільш доходний, результати розрахунків занесемо у таблицю 3.2.
Таблиця 3.2.
Розрахунок наступної вартості внеску при різних умовах інвестування
| № варіанту | Поточна вартість внеску | Ставка відсотку | Наступна вартість у кінці | |||
| 1 – го періоду | 2 – го періоду | 3 – го періоду | 4 – го періоду | |||
| - | - - | - - - |
Порівняння варіантів показує, що найбільш ефективним є 1-й варіант (виплата доходу у розмірі 23% на квартал).
Слід зауважити, що періодичність нарахування відсотків також впливає на величину накопичення. Якщо внесок у сумі 100 тис. грн. зберігати два роки у банку, який нараховує 24% річних (під складний відсоток), то в залежності від періодичності нарахування накоплена сума буде складати:
а) щорічне нарахування відсотків (два рази по 24%)
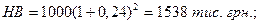
б) піврічне нарахування відсотків (чотири рази по 12%)
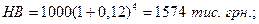
в) щоквартальне нарахування відсотків (вісім разів по 6%)
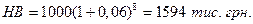
Таким чином, при інших рівних умовах, чим частіше нараховуються відсотки, тім більше буде накопичена сума.
Функція «дисконтування»
Функція «дисконтування» дозволяє визначити поточну (теперішню чи приведену) вартість суми, якщо відома її величина у майбутньому при даному періоді накопичення і відсотковій ставці
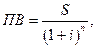
де ПВ - поточна вартість; S - відома у майбутньому сума; i - відсоткова ставка; n - число періодів нарахування відсотків.
Множник 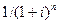 називають коефіцієнтом дисконтування.
називають коефіцієнтом дисконтування.
Функція «дисконтування» є зворотною по відношенню до функції «складного відсотку». Значення коефіцієнтів дисконтування для різних відсоткових ставок і числа періодів нарахування відсотків приведені у табличному виді у додатку А.
Задача. Яку суму необхідно вкласти на депозит під 10% річних, щоб через 5 років накопичити 1500 тис. грн.?
Рішення. Розраховуємо поточну вартість суми
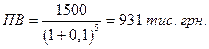
Таким чином, інвестування 931 тис. грн. на 5 років при ставці доходу 10% забезпечить накопичення у сумі 1500 тис. грн.
Задача. Інвестиційний проект дозволяє отримати 100 тис. грн. (ставка доходності 20% річних), 150 тис. грн. (ставка доходності 25% річних) та 200 тис. грн. (ставка доходності 30% річних). Яка сума необхідна у теперішній час для реалізації інвестиційного проекту?
Рішення. Розрахуємо поточну вартість суми
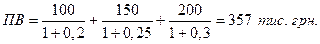
Таким чином, інвестування у проект 357 тис. грн. на один рік забезпечить доход у 100+150+200=450 тис. грн.
Для ілюстрації понять поточна і майбутня вартості розглянемо приклад, коли інвестиції фінансуються за рахунок позикового капіталу, який припускає первісні вкладення 10 тис. грн., доход через рік 11, 506 тис. грн., відсоткову ставку 10%.
Припустимо, що інвестор вирішив запозичити потрібну для інвестування суму і вилучити свій наступний доход тільки після погашення боргу. Через рік інвестор повинен повернути кредитору (10 + 10  0, 1) = 11 тис. грн. Тоді інвестор отримає через рік чистий майбутній доход у 506 грн.
0, 1) = 11 тис. грн. Тоді інвестор отримає через рік чистий майбутній доход у 506 грн.
Припустимо, що по тим чи іншим причинам інвестор віддасть перевагу отримати доход не через рік, а зараз. Розрахуємо поточну вартість доходу, яка становитиме 11, 506: (1 + 0, 1) = =10, 460 тис. грн. Тоді чиста поточна вартість доходу, яка дорівнює 10, 460 - 10 = 460 грн. чи 506: (1 + 0, 1) = 406 грн. Отже, інвестор може взяти у кредит 10, 460 тис. грн. під 10% річних, з них 10 тис. грн. - направити на інвестиції, а 460 грн. відразу вилучити на споживання. Через рік інвестор повинен повернути 11, 506 тис. грн.
Таким чином, у інвестора є дві можливості: отримати доход 460 грн. у теперішній час або 506 грн. через рік.
Функція «поточна вартість ануітету»
Ануітет може бути вихідним грошовим потоком по відношенню до інвестора (наприклад, здійснення періодичних рівних платежів за отриманий кредит) або вхідним грошовим потоком (наприклад, надхождення арендної плати, розмір якої, зазавичай, фіксований).
При розрахунку поточної вартості ануітету, який здіснюється на умовах попередніх платежів (при внесенні платежів на початку року) використовується формула
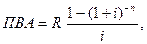
де ПВА - поточна вартість ануітету, який здіснюється на умовах попередніх платежів; R - розмір окремого платежу; i - відсоткова ставка; n - число періодів нарахування відсотків.
Задача. Яку суму необхідно покласти на депозит під 10% річних, щоб потім щороку пять разів зняти по 300 тис. грн.?
Рішення. Розраховуємо поточну вартість ануітету
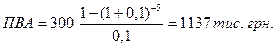
Таким чином, наступна вартість 5  300 = 1500 тис. грн. еквивалентна поточній вартості ануітету 1137 тис. грн. Перевіремо данне твердження методом депозитної книжки (табл. 3.3)
300 = 1500 тис. грн. еквивалентна поточній вартості ануітету 1137 тис. грн. Перевіремо данне твердження методом депозитної книжки (табл. 3.3)
Таблиця 3.3
Депозитна книжка
| Рік | Залишок на початок року, тис. грн. | Плюс 10% на залишок, тис. грн. | Мінус річне вилучення, тис. грн. | Залишок на кінець року, тис. грн. |
| Перший Другий Третій Четвертий П’ятий |
Функція «періодичний внесок на погашення кредиту»
Часова оцінка грошових потоків може поставити перед аналітиком проблему визначення розміру окремого платежу, якщо відома поточна вартість ануітету, кількість платежів і дисконтна ставка.
Функція періодичного внеску на погашення кредиту є зворотньою по відношенню до функції поточної вартості ануітету
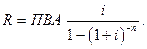
Задача. Розрахувати розмір платежу для погашення кредиту при наступних вихідних даних: поточна вартість ануітету (кредиту) 100 тис. грн.; період платежів з ануітету 5 років; інтервал платежів з ануітету складє один рік (при внесенні платежів на початку року); відсоткова ставка складає 10%. Перевірити отриманий результат з використанням плану погашення кредиту.
Рішення. Періодичний внесок на погашення кредиту складає
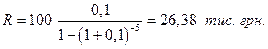
Таким чином, для погашення кредиту 100 тис. грн. протягом 5 років при відсотковій ставці 10% потрібен щорічний внесок 26, 38 тис. грн.
Перевіримо дане твердження з використанням плану погашення кредиту (табл.3.4).
Таблиця 3.4
План погашення кредиту
| Рік | Вартість кредиту на початок поточного року, тис. грн. | Вартість кредиту на початок наступного року, тис. грн. | Внесок на початку наступного року, тис. грн. |
| Перший Другий Третій Четвертий П’ятий Шостий | 83, 62 65, 6 45, 78 23, 98 | 91, 98 72, 16 50, 36 26, 38 | 26, 38 26, 38 26, 38 26, 38 26, 38 |
Одержувач позики сплатить кредитору за 5 років 5  26, 38 = 131, 9 тис. грн., що перевищує величину виданого кредиту на 131, 9 - 100 = 31, 9 тис. грн. Різниця є сумою відсотків, які сплачені одержувачем позики за період кредитування, при умові, що основний борг постійно зменшується.
26, 38 = 131, 9 тис. грн., що перевищує величину виданого кредиту на 131, 9 - 100 = 31, 9 тис. грн. Різниця є сумою відсотків, які сплачені одержувачем позики за період кредитування, при умові, що основний борг постійно зменшується.
Задача. Яку суму можна щорічно знімати з рахунку протягом п’яти років, якщо первісний внесок дорівнює 1500 тис. грн.? Банк нараховує щорічно 14% і при умові, що суми, які знимаються, будуть однакові. Перевірити отриманий результат методом депозитної книжки.
Рішення. Сума, яку можна щорічно знімати з рахунку, складає
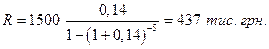
Таким чином, якщо покласти на рахунок під 14% річних 1500 тис. грн., можна п’ять раз зняти по 437 тис. грн. Додаткові отримані гроші в сумі 437  5 - 1500 = 685 тис. грн. є результатом нарахування відсотків на залишок внеску, який зменшується.
5 - 1500 = 685 тис. грн. є результатом нарахування відсотків на залишок внеску, який зменшується.
Перевіримо дане твердження методом депозитної книжки (табл. 3.5)
Таблиця 3.5
Депозитна книжка
| Рік | Вартість вкладу на початок року, тис. грн. | Вартість вкладу на кінець року, тис. грн. | Сума, яка щорічно знимається з рахунку, тис. грн. |
| Перший Другий Третій Четвертий П’ятий Шостий |
Функція «майбутня вартість ануітету»
Ця функція дозволяє розрахувати величину накопичених рівновеликих внесков при заданої ставки доходу
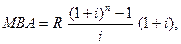
де МВА - майбутня вартість ануітету, якій здіснюється на умовах попередніх платежів.
Задача. Яка сума буде накопичена на рахунку, якщо протягом четирьох років щорічно вносити по 350 тис. грн., а банк нараховує на внесок 6% річних? Перевірити отриманий результат методом депозитної книжки.
Рішення.
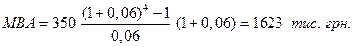
Таким чином, депонування 350  4 =1400 тис. грн. забезпечує накопичення через чотири роки 1623 тис. грн. Різниця 1623 - 1400 = 223 тис. грн. є доходом з відсотків, які нараховані за технікою складного відсотку на суму, що зростає.
4 =1400 тис. грн. забезпечує накопичення через чотири роки 1623 тис. грн. Різниця 1623 - 1400 = 223 тис. грн. є доходом з відсотків, які нараховані за технікою складного відсотку на суму, що зростає.
Перевіримо дане твердження методом депозитної книжки (табл. 3.6).
Таблиця 3.6
Депозитна книжка
| Рік | Внесок на початок поточного року, тис. грн. | Вартість внеску на кінець поточного року, тис. грн. | Вартість внеску на кінець наступного року, тис. грн. |
| Перший Другий Третій Четвертий |
Задача. Яка сума буде накопичена на рахунку, якщо протягом п’яти років щорічно вкладати по 100 тис. грн., а банк нараховує на внесок 10% річних? Перевірити отриманий результат методом депозитної книжки.
Рішення.
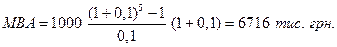
Таким чином, депонування 1000  5 = 5000 тис. грн. забезпечує накопичення через 5 років 6716 тис. грн. Різниця 6716 - 5000 = 1716 тис. грн. є доходом з відсотків, які нараховані за технікою складного відсотку на суму, що зростає.
5 = 5000 тис. грн. забезпечує накопичення через 5 років 6716 тис. грн. Різниця 6716 - 5000 = 1716 тис. грн. є доходом з відсотків, які нараховані за технікою складного відсотку на суму, що зростає.
Перевіримо дане твердження методом депозитної книжки (табл. 3.7).
Таблиця 3.7
Депозитна книжка
| Рік | Внесок на початок поточного року, тис. грн. | Вартість внеску на кінець поточного року, тис. грн. | Вартість внеску на початок наступного року, тис. грн. |
| Перший Другий Третій Четвертий П’ятий |
Функція «періодичний внесок на накопичення фонду»
Функція «переодичний внесок на накопичення фонду» є зворотньою по відношенню до функції «майбутня вартість ануітету». Ця функція дозволяє розраховувати величину внеску (розміру окремого платежу, члену ануітету), який потрібен для накопичення зумовленої суми при заданій ставці відсотку
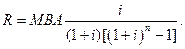
Задача. Яку суму потрібно щорічно вкладати на депозит, що поповнюється, під 8% річних, щоб накопичити за 5 років 1700 тис. грн.? Перевірити отриманий результат методом депозитної книжки.
Рішення.
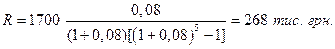
Таким чином, сумарний внесок в 268  5 = 1340 тис. грн. при нарахуванні 8% річних дозволяє накопичити 1700 тис. грн.
5 = 1340 тис. грн. при нарахуванні 8% річних дозволяє накопичити 1700 тис. грн.
Перевіримо дане тверження методом депозитної книжки (табл. 3.8).
Таблиця 3.8
Депозитна книжка
| Рік | Внесок на початок поточного року, тис. грн. | Вартість внеску на кінець поточного року, тис. грн. | Вартість внеску на кінець наступного року, тис. грн. |
| Перший Другий Третій Четвертий П’ятий |